Podstawy reakcyjnej i predykcyjnej regulacji PID - Część 1

Sterowanie obiektem lub inną złożoną maszyną wymaga zdefiniowania planu lub modelu celu, który ma zostać zrealizowany. Zadaniem układu sterowania jest porównywanie zdefiniowanego modelu z rzeczywistością oraz przekazywanie poleceń do serwonapędów lub innych urządzeń wykonawczych, aby rzeczywistość podążała za planem. Oczekiwana temperatura obiektu lub pozycja siłownika jest określana mianem wartości zadanej, a obecna wartość tych sygnałów – mianem wartości mierzonej.

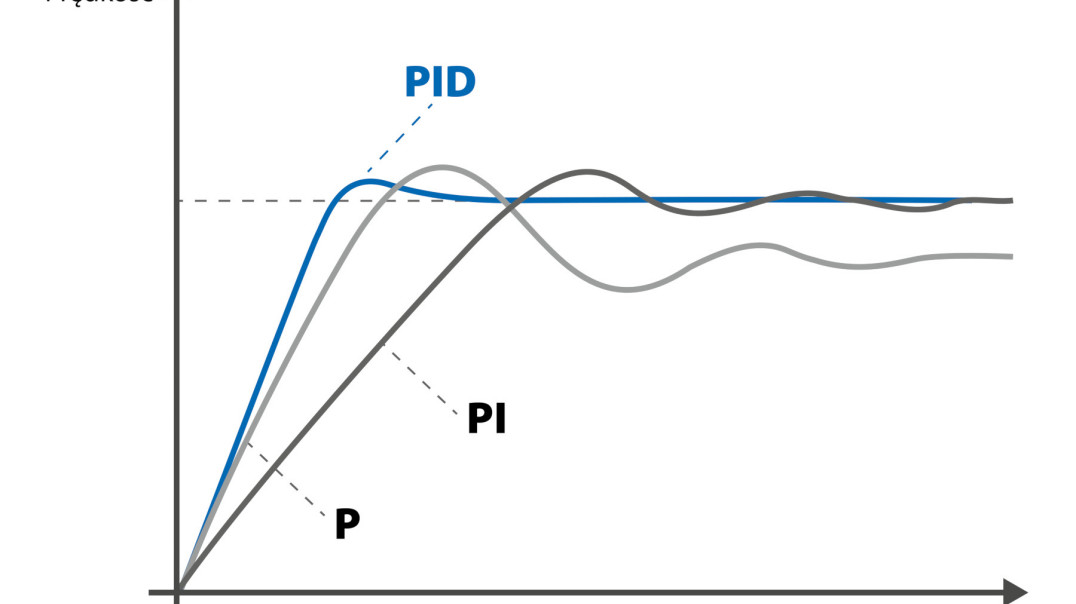
Zamknięty układ sterowania mierzy różnicę między wartością zadaną i mierzoną, po czym próbuje ją zmniejszyć zgodnie z określonym algorytmem. W rzeczywistości chodzi o to, aby układ sterowania zapewnił maksymalnie szybką odpowiedź na zmieniające się sygnały wejściowe bez powodowania oscylacji.

Klasyczna teoria sterowania skupia się na obserwacji odpowiedzi układu na skokową zmianę sygnału wejściowego. Jednak bardzo trudne jest zbudowanie układu regulacji, który szybko i bez przeregulowania zareaguje na tego typu wejście. Naczelna zasada przy sterowaniu programowym polega na tym, aby nie realizować takiego sterowania, w którym wartość zadana nie może być dokładnie śledzona.

Z analizy matematycznej wiadomo, że położenie jest całką prędkości (a więc w pewnym sensie jej uśrednieniem), a prędkość – całką z przyspieszenia, podczas gdy celem analizy jest określenie przyszłych zależności między tymi zmiennymi. Jednak w aplikacjach sterowania w czasie rzeczywistym taka predykcja nie jest z reguły wymagana. Zamiast tego czas jest dzielony na niewielkie przedziały, w których rejestruje się przyspieszenie wykorzystywane do uzyskania prędkości, na podstawie której oblicza się pozycję. I jeśli wyznaczone zmienne znajdują się w zakresie realizowanym przez oprzyrządowanie, możliwe jest zaprojektowanie układu sterowania dokładnie śledzącego wartość zadaną.

Częstym problemem w przypadku klasycznej teorii sterowania jest to, że wymagane parametry są nieznane lub ulegają zmianom podczas pracy. Na przykład bezwładność robota zależy od wielu składowych, takich jak obrotowa bezwładność wirnika i opon, bezwładność przekładni i wałów oraz wynikająca z masy i ładunku. Ponadto pomiędzy elementami robota mogą znajdować się łożyska i przekładnie, które charakteryzują się sprężystością czy tarciem.

Dokładne zamodelowanie dynamiki bardzo złożonych układów jest z reguły niepraktyczne ze względu na wiele zmiennych i niewiadomych. Dlatego inżynierowie szukają prostszych technik.

Algorytm PID

Sterowanie PID jest typowo reakcyjne, gdyż wytwarzany sygnał sterujący zależy tylko od wartości uchybu. Regulatory tego typu zostały po raz pierwszy zastosowane w przemyśle w zamkniętych układach regulacji temperatury i były projektowane z wykorzystaniem komponentów analogowych.

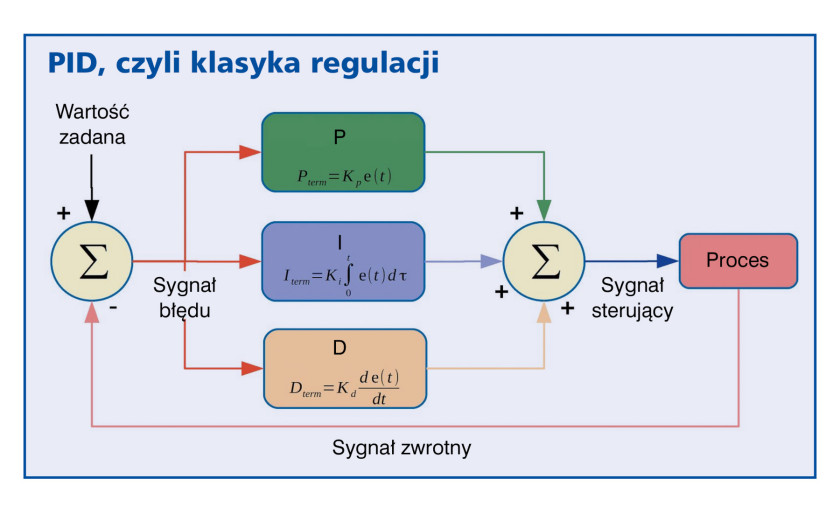
Programowe regulatory PID są dzięki swojej prostocie implementowane do aplikacji serwonapędowych, w systemach ogrzewania i podobnych. Na rysunku 1 przedstawiono uproszczony schemat blokowy regulatora PID.

 

Rys. 1 Klasyczny analogowy regulator PID

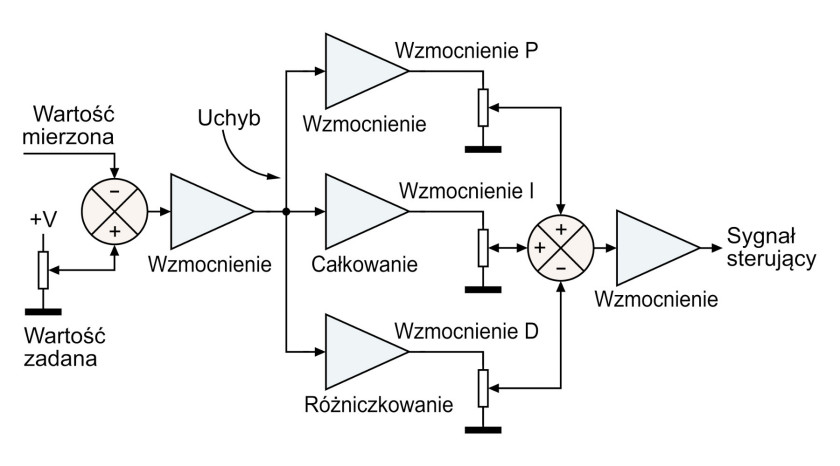
Ponieważ w układach regulacji silników niektóre składowe regulatora PID nie działają optymalnie, przedstawione w artykule wykresy dotyczą regulacji temperatury.

Regulator PID składa się z trzech oddzielnych bloków, których wyjścia są sumowane do postaci jednego sygnału sterującego. Bieżący odczyt sygnału regulowanego jest odejmowany od wartości zadanej (w tym przypadku ustawionej za pomocą potencjometru) celem wytworzenia sygnału uchybu, który jest następnie przetwarzany przez trzy procesory sygnałowe.

Regulator PID - część proporcjonalna (P)

Pierwszym procesorem sygnałowym jest prosty wzmacniacz. Część proporcjonalna mogłaby być stosowana samodzielnie, ale tylko w najprostszych przypadkach, ponieważ w momencie gdy wartość mierzona osiąga wartość zadaną, sygnał uchybu będzie równy zero.

Należy pamiętać, że pomiar sygnału regulowanego jest opóźniony w stosunku do czasu wygenerowania sygnału sterującego przez regulator. Jeśli wzmocnienie części proporcjonalnej będzie zbyt duże, to podczas próby minimalizacji uchybu układ wejdzie w oscylacje. Zatem prosty wzmacniacz nie pozwala na dokładne śledzenie wartości zadanej i tym samym całkowitą likwidację uchybu w stanie ustalonym (rys. 2).

 

Rys. 2 Jakość regulacji P

Regulator PID - część całkująca (I)

Umieszczenie członu całkującego w układzie spowoduje powolny, lecz stały wzrost lub spadek sygnału wyjściowego w przypadku niezerowego uchybu. Gdy uchyb zostanie zlikwidowany, część całkująca przestanie ulegać zmianom. Należy jednak pamiętać, że osiągnięcie zerowego błędu statycznego wymaga czasu.

Ponieważ część całkująca wprowadza do pętli dodatkowe opóźnienie, w przypadku jej zbyt dużego wzmocnienia powstaną oscylacje o częstotliwości mniejszej od tych spowodowanych przez część proporcjonalną. Dlatego akcję proporcjonalną stosuje się do uzyskania szybkiej odpowiedzi, podczas gdy część całkująca zapewnia dużą dokładność w długim okresie.

Słabym punktem części całkującej jest zjawisko określane mianem wind-up. Duża zmiana wartości zadanej przyczynia się do gromadzenia w rejestrze całkującym zbyt dużej wartości sygnału, zbędnej w stanie ustalonym. Z tego powodu, gdy sygnał mierzony osiągnie wartość zadaną, w układzie zacznie pojawiać się przeregulowanie, ponieważ algorytm nie będzie w stanie szybko opróżnić rejestru, w którym zgromadzone zostały próbki wartości wynikające z poprzednich operacji całkowania.

W ogólnym przypadku część całkująca jest lepiej przystosowana do regulacji temperatury niż w aplikacjach napędowych, szczególnie w robotach mobilnych, gdzie wartości zadane serwonapędów ulegają ciągłym zmianom.

W aplikacjach napędowych zadawane prędkości zmieniają się tak gwałtownie, że część całkująca nie jest w stanie zlikwidować uchybu. Z tego powodu nie poleca się stosowania składowej całkującej w układach sterowania, w których sygnał sterujący będzie równy zero w chwili osiągnięcia wartości zadanej przez sygnał mierzony, co ma miejsce przy sterowaniu ruchem robota na płaskiej powierzchni.

W aplikacjach, gdzie użycie części całkującej jest celowe, a wartość zadana w długich okresach pozostaje stała, przydatne jest z reguły całkowanie na żądanie. W takiej sytuacji prosty układ logiczny obserwuje wartość zadaną i jeśli jest ona stała, czyli jej pochodna jest dostatecznie mała, część całkująca zostaje aktywowana. Jeśli wartość zadana będzie w trakcie zmiany, to rejestr części całkującej zostanie niezmieniony lub opróżniony.

Z reguły jednak wprowadzenie nagłych zmian podczas obliczeń algorytmu PID, takich jak np. opróżnienie rejestru całkowania, nie jest rozwiązaniem optymalnym, ponieważ skutkuje to destabilizacją układu.

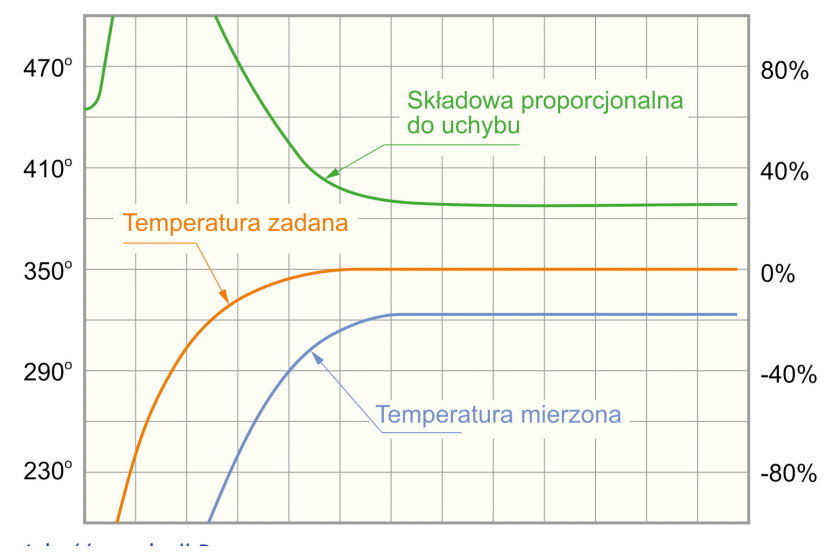
Na rysunku 3 przedstawiono przebiegi sygnałów z układu sterowania PID wykorzystującego tylko części P oraz I o odpowiednio dobranych nastawach. Skala prawa odnosi się do składowej proporcjonalnej do uchybu, całkującej uchyb oraz wartości sygnału sterującego, podczas gdy lewa dotyczy temperatury zadanej oraz temperatury mierzonej.

 

Rys. 3 Regulacja PID z wykorzystaniem jedynie części proporcjonalnej i całkującej

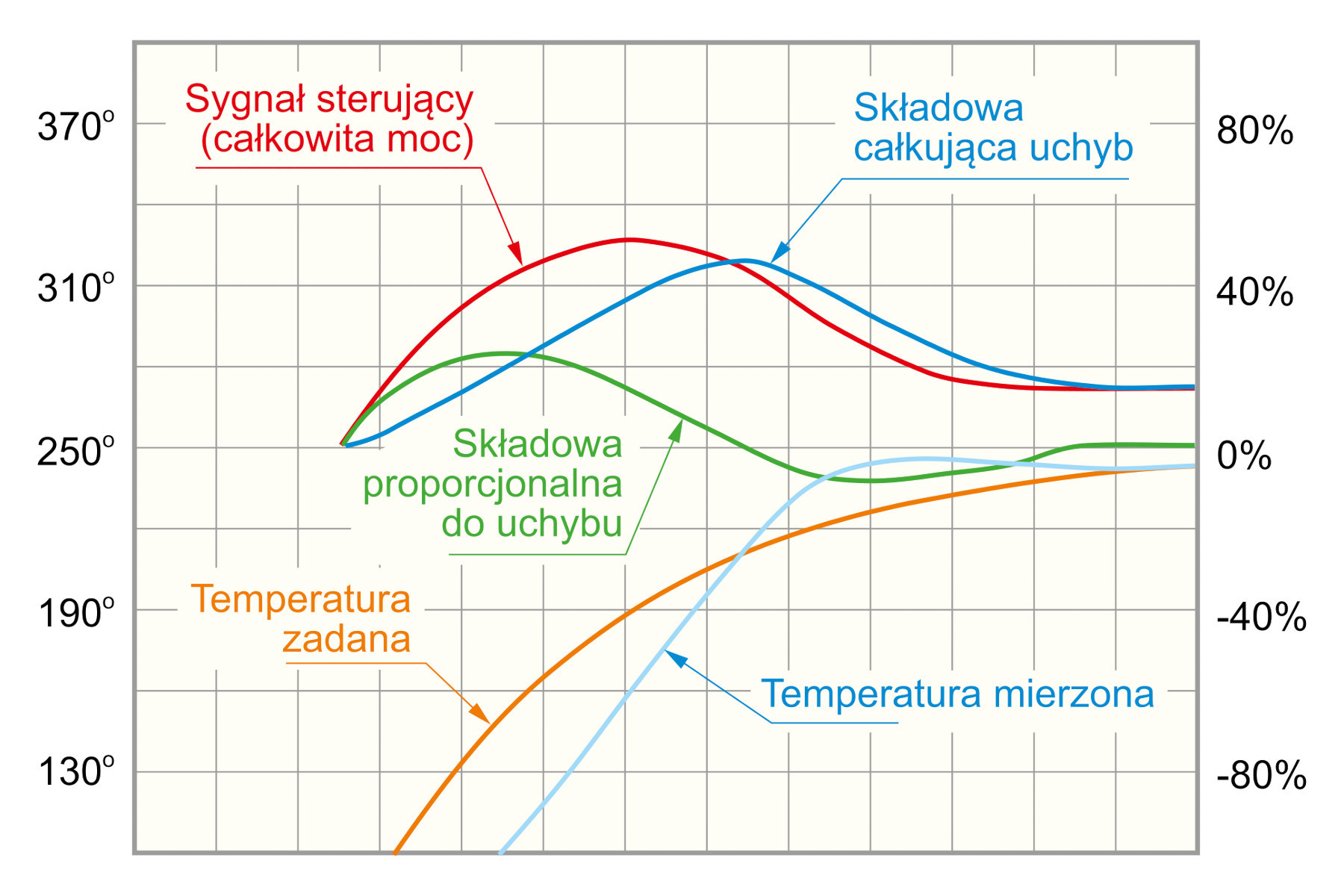
Należy zauważyć, że temperatura zadana jest funkcją wykładniczą, której wartość osiąga 250°. I mimo że temperatura mierzona w stanie przejściowym wyraźnie przekracza wartość zadaną, to prawie dokładnie osiąga ją w stanie ustalonym. Przekroczenie wartości zadanej powoduje, że wyjście części proporcjonalnej staje się ujemne, co spowalnia zbliżanie się do wartości końcowej. Część całkująca generuje duży sygnał podczas wznoszenia się wartości zadanej, a jej wpływ jest neutralizowany przez część proporcjonalną.

Jakość takiego układu będzie jednak optymalna tylko w przypadku, dla którego zostały dobrane nastawy regulatora. Gdyby wartość zadana zamiast do 250°, dążyła do 350°, powstałoby znaczące przeregulowanie spowodowane zbyt dużym sygnałem wygenerowanym przez część całkującą. Ponieważ napędy serwomechanizmów muszą operować w szerokim zakresie położeń i prędkości, w takich aplikacjach pożądane byłoby zastosowanie metod sterowania odpornego.

Regulator PID - część różniczkująca (D)

Ponieważ części P oraz I mają tendencję do powodowania oscylacji, naturalne jest poszukiwanie elementu, który to zjawisko zrównoważy. Tym zajmuje się składowa różniczkująca D, która generuje sygnał proporcjonalny do pochodnej uchybu lub innymi słowy – do szybkości zmiany uchybu.

Część ta jest odejmowana od pozostałych, aby wytłumić zmiany błędu. Zatem wartość wymaganego sygnału sterującego regulatora PID może być opisana równaniem:

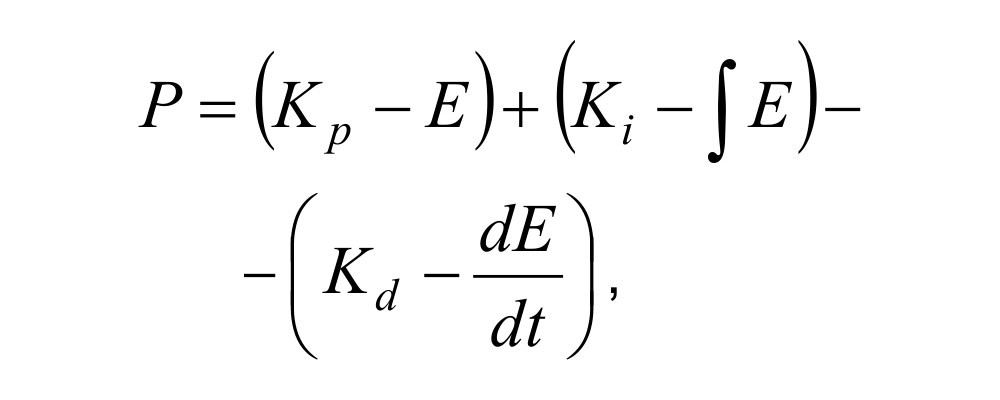
gdzie E to uchyb chwilowy, a K_p, K_i, K_d – współczynniki wzmocnienia składowej proporcjonalnej, całkującej i różniczkującej.

Implementacja algorytmu PID

Implementacja algorytmu PID następuje przez wielokrotne wykonywanie podprogramu obliczeniowego z częstotliwością zależną od czasu trwania odpowiedzi układu. Im większa częstotliwość, tym szybciej napęd może odpowiedzieć, co jednak wymaga większych zasobów obliczeniowych. W ogólnym przypadku szybkość działania algorytmu PID do sterowania ruchem serwomechanizmu lub robota mobilnego, poruszającego się wolniej niż 5 km/h, powinna wynosić między 10 a 100 Hz.

Wartość składowej proporcjonalnej jest wynikiem prostego, natychmiastowego odejmowania. Z kolei całkowanie polega na mnożeniu uchybu chwilowego przez wzmocnienie części całkującej oraz dodaniu wyniku do rejestru akumulatora. W przypadku ujemnego uchybu efekt całkowania będzie realizowany przez odejmowanie obliczonej wartości od rejestru akumulatora.

Pochodną oblicza się poprzez odjęcie od obecnego uchybu wartości uchybu z chwili poprzedniej. W niektórych przypadkach jednak wynik może być niedokładny, zatem bardziej pożądane jest uśrednianie obecnego wyniku z kilkoma poprzednimi.

Niestety, składowa różniczkująca również może przyczynić się do niestabilności, jeśli jej efektywne wzmocnienie będzie większe od jedności i wzmocnione zostaną szumy występujące w układzie. Znaczenie składowej różniczkującej w układach regulacji temperatury jest niewielkie, podobnie jak w aplikacjach serwonapędowych, w których zastosowanie czysto reakcyjnej regulacji typu PID jest dość ograniczone.

Zobacz kontynuację omówienia regulacji PID

W drugiej części artykułu omówione zostaną przykłady predykcyjnej i reakcyjnej regulacji, a także implementacje PID w systemach regulacji temperatury oraz sterowania ruchem.

Grzegorz Michałowski