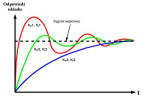
Konieczność stosowania regulatorów podyktowana jest fizycznymi właściwościami obiektów i regulowanych elementów. Przykładowo niemożliwe jest natychmiastowe zwiększenie szybkości pracy linii produkcyjnej lub jej przejście ze stanu spoczynku do pożądanej prędkości. Aby zapewnić płynną zmianę tych wartości pomiędzy stanem obiektu w momencie podania sygnału sterującego, a chwilą gdy osiągnie on parametry docelowe, stosuje się regulatory. Fakt ten jest dla czytelników z pewnością oczywisty, tak samo jak możliwość wydzielenia w konwencjonalnych regulatorach PID trzech bloków odpowiedzialnych za działanie proporcjonalne (odpowiadająca za wzmacnianie sygnału), całkujące (odporność na zakłócenia wolnozmienne i możliwość uzyskania zerowego uchybu) oraz różniczkujące (m.in. tłumienie szybkich zakłóceń). W praktyce wykorzystuje się różne kombinacje tych bloków, stąd też nazwy regulatorów – P, PI, PD oraz PID. Poniżej przedstawione zostało porównanie właściwości konwencjonalnego regulatora PI oraz regulatora wykorzystującego logikę rozmytą (fuzzy logic).
Słowo o regulacji klasycznej
Konwencjonalne regulatory proporcjonalno-całkujące (PI) charakteryzują się stałymi wzmocnieniami obydwu wykorzystywanych w nich bloków w całym zakresie wartości wejściowych. Wartością wejściową jest najczęściej uchyb, czyli różnica pomiędzy sygnałem zadanym i wyjściowym układu. Odpowiedź systemu jest definiowana jako reakcja na zmianę wartości zadanej lub na zakłócenia zewnętrzne. Zadaniem projektanta jest takie dobranie parametrów regulatora aby możliwie najszybciej zminimalizowany został uchyb, oczywiście przy zachowaniu stawianych ograniczeń w postaci dopuszczalnego maksymalnego przeregulowania oraz wymaganej precyzji.
Logika rozmyta
O ile teoria związana z logiką rozmytą należy do zaawansowanych dziedzin matematyki, jej podstawy można wyjaśnić w przystępny sposób. Próbując przykładowo sklasyfikować za pomocą logiki klasycznej miesiące pod względem przynależności do pór roku pojawiają się cztery kłopotliwe miesiące. Nie można bowiem powiedzieć, że stwierdzenie „czerwiec jest miesiącem wiosennym” to prawda, jest to bowiem „prawie prawda”. Z pomocą przychodzi logika rozmyta, w której przynależność do danego zbioru jest określana dodatkowym parametrem - tzw. funkcją przynależności, która przybiera wartości od 0 do 1. W reprezentacji graficznej charakteryzuje się ona też określonym kształtem. Wykorzystując logikę rozmytą można powiedzieć, że „czerwiec należy do wiosny” to prawda w dwóch-trzecich, czyli funkcja przynależności elementu „czerwiec” do zbioru „wiosna” równa się 2/3.

Funkcje przynależności
W zależności od potrzeb funkcję przynależności można tak wyznaczyć, aby uzyskać szybszą zmianę wzmocnienia gdy wartość błędu jest wysoka. Można też skoncentrować się na zwiększeniu precyzji, czyli zróżnicowaniu działania regulatora gdy wartość błędu jest niewielka. W obydwu przypadkach możliwe jest zachowanie wszystkich parametrów na zadowalającym poziomie - np. szybkiego czasu reakcji przy niewielkim przesterowaniu. Zaletą tej techniki jest uproszczenie opisu systemu oraz możliwość względnie łatwego zaprojektowania i implementacji dowolnej zależności pomiędzy wejściem a wyjściem układu.
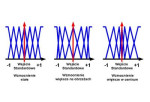
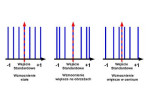
Na rys. 2 przedstawiono przykłady funkcji przynależności dla sytuacji gdy użytkownik chce uzyskiwać stałe wzmocnienie dla wszystkich wartości wejściowych oraz dwa przypadki nieliniowe. Efektywne wzmocnienie obliczane jest na podstawie wartości funkcji przynależności w danym punkcie i jest to najczęściej wynik oceny z użyciem wypadkowej dwóch reguł. Dla zmniejszenia potrzebnej mocy obliczeniowej można zastąpić trójkątną postać funkcji przynależności impulsami, tak jak zostało to przedstawione na rys. 3.
Zalety, ale też wady
Zaprojektowanie układu regulacji wykorzystującego logikę rozmytą polega na określeniu szeregu reguł dla różnych wartości sygnału wejściowego. Przykładowo założyć można że wartości w okolicach 50 (np. milimetrów) powoduje, że regulator ma charakterystykę liniową, wartości około 25mm zwiększają zwiększanie się funkcji przynależności w centrum, natomiast wartość powyżej 60mm powoduje zwiększanie się wartości funkcji przy granicach rozważanego zakresu, tak jak jest to pokazane na rys. 2 i 3. Niemniej nawet w tak prostym przypadku wymagane jest dopasowanie ośmiu zmiennych - po cztery dla wejścia i wyjścia. Konieczne jest również wybranie zakresu wejściowego dla każdego wejścia i przeskalowanie wzmocnień części P oraz I regulatora, tak aby uzyskać wymagany efekt końcowy.
Nieliniowy regulator PI
Modyfikacja bloku PI
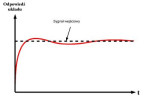
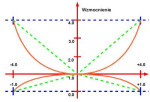
Wymienione powyżej wymagania można spełnić poprzez wprowadzenie dwóch parametrów – odpowiedzialnego za dostrojenie kształtu oraz za skalowanie funkcji przejścia. Parametry te są oddzielne dla części P oraz I (patrz rys. 5 – linia ciągła to funkcja paraboliczna, przerywana – funkcja liniowa). Otrzymujemy się wtedy dwa równania:
* Dla części proporcjonalnej: y=(Kształt_P–1)*x²+1
* Dla części całkującej: y=(Kształt_I–1)*x²+1
W równaniach tych wartość y jest wynikiem przemnożenia tradycyjnie dobranego KP/KI przez odpowiednią wartość, która zależy od wielkości uchybu. W omawianym przypadku jest to liczba z zakresu <4,0>. Wartość b jest stała i wynosi 1, co jest spowodowane wymogiem, aby dla zerowego błędu wartość wzmocnień nie była zmieniana. Parametry Kształt_P i Kształt_I są związane z kształtem funkcji przejścia, z kolei zmienna x jest stosunkiem wartości wejściowej do rozważanego zakresu błędu i przyjmuje wartości <-1,1>. Dla ułatwienia obliczeń można przyjąć jej zakres jako <0,1>.

Podsumowanie
Porównując trudności jakie niesie ze sobą użycie wnioskowania wykorzystującego logikę rozmytą z metodą modyfikacji konwencjonalnego regulatora PI poprzez przeskalowanie wartości wzmocnień przy użyciu funkcji przejścia, można dojść do wniosku, że drugie z rozwiązań wymaga mniejszych nakładów obliczeniowych. Z pewnością obydwie metody mogą jednak dawać lepsze wyniki niż te wykorzystujące konwencjonalne. Staje się to tym istotniejsze wraz ze wzrostem stopnia złożoności obiektu sterowania.
Wojciech Adamski













