W bardziej zaawansowanych systemach brane są pod uwagę charakterystyki napędu i wykorzystywane złożone algorytmy. Dodatkowo różne typy silników i napędów charakteryzują się różnymi parametrami, co powoduje, że zależnie od aplikacji stosowane są różne metody sterowania i regulacji.
Sterowanie ruchem odbywa się w wielu aplikacjach przemysłowych w podobny sposób. Sygnał generowany przez przycisk start może być przetwarzany przez sterownik 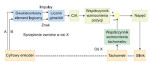
Rys. 1. Sprzężenie zwrotne jako podstawa układu sterowania
Pętla sprzężenia zwrotnego jest kluczowym elementem precyzyjnej regulacji ruchu. Na rys. 1 przedstawiono pętlę sprzężenia zwrotnego z cyfrowym 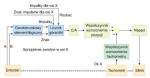
Rys. 2. Układ sterowania uwzględniający tory rozkazów impulsowych
Pierwsze obrabiarki numeryczne z lat 60. zeszłego wieku oprócz pętli sprzężenia zwrotnego wykorzystywały skoordynowane ciągi rozkazów impulsowych. Każdy licznik miał dwa dodatkowe wejścia: tor rozkazów impulsowych oraz tor znaku. Po przekazaniu rozkazów impulsowych ze znakiem „+” do licznika, jego wartość zwiększała się i generowany był sygnał do napędu silnika, co z kolei powodowało powstanie w sprzężeniu zwrotnym impulsów ze znakiem „–”, co z kolei zmniejszało wartość licznika. Podczas ruchu stan licznika równy był błędowi śledzenia. Gdy ustawały rozkazy impulsowe, wartość licznika powracała do zera a ruch kończył się.
Na rys. 2 przedstawiono układ sterowania uwzględniający dodatkowe tory rozkazów impulsowych, zaprojektowane w taki sposób, aby zapobiec przypadkowemu pominięciu jakichkolwiek impulsów. Przykładowo, jeśli rozkaz ze znakiem „+” oraz sygnał sprzężenia zwrotnego „–” wystąpią jednocześnie, żaden impuls zliczający nie zostanie przekazany do licznika. Natomiast jeśli oba sygnały wystąpią ze znakiem „+”, wartość licznika zwiększy się o 2.
Wczesne obrabiarki sterowane numerycznie używały mnożników częstotliwości dla poszczególnych osi, a urządzenia wykonawcze sterowane były liczbą impulsów zależną od zaprogramowanego rozkazu.
Modulacja rozkazów
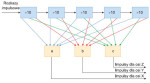
Rys. 3. Dzielnik impulsów
Ponieważ w obecnie dostępnych systemach rozkazy przeznaczone dla każdej osi pochodzą ze wspólnego dzielnika impulsów (rys. 3), wykonywane ruchy są jednoczesne i dla każdej osi proporcjonalne do czasu, jaki upłynął od rozpoczęcia ruchu. Współczynniki proporcjonalności określone są jednak osobno dla poszczególnych osi jako: x=at, y=bt, z=ct
Z kolei prędkość propagacji określana jest na podstawie częstotliwości impulsów źródłowych. Wynosić ona może np. 100kHz (jeden impuls na 10µs), a rozkaz impulsowy ma taką samą rozdzielczość jak impuls sprzężenia zwrotnego z opisanego wcześniej enkodera cyfrowego.
Modulator programowy
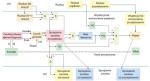
Rys. 4. Cyfrowe sprzężenie zwrotne zamiast fizycznego tachometru
W celu zamiany sprzętowego modulatora impulsów na instrukcję komputerową należy zamienić powyższe równanie na postać różniczkową. Załóżmy, że zmienna „t” w równaniu reprezentuje czas równy długości jednego impulsu źródłowego powtarzającego się co 10µs, a równanie jest wykonywane 10 tys. razy. Jeśli zamiast t=10µs przyjmie się ∆t=1ms, całkowita liczba iteracji zmniejszy się 100 razy. Należy więc pomnożyć współczynniki a, b i c przez 100, aby uzyskać taki sam ruch. W związku z tym powstaną nowe stałe A, B i C, odpowiednio o wartościach 72,42, 42,96 i 15,48: x=A∆t, y=B∆t, z=C∆t
Innymi słowy, dla jednej iteracji o wartości 1ms, ruch w każdej osi musi być odpowiednikiem 72, 42 i 15 impulsów, natomiast części ułamkowe zostaną przeniesione do następnej iteracji.
Często zamiast współrzędnych względnych (∆x, ∆y, ∆z) używanych do określenia celu sterowania, wykorzystywane są współrzędne absolutne (x, y, z), które wystarczają do większości zastosowań związanych z ruchem.
Programowa realizacja układu
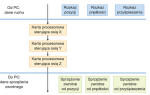
Rys. 5. Zadania komputera oraz kart procesorowych
W zaawansowanych systemach sterowania po zadanej trajektorii można dodatkowo zaprogramować pętlę prędkości i przyspieszenia. Na rys. 4 przedstawiono cyfrowe sprzężenia zwrotne oraz sterowanie rozkazami w takiej sytuacji. Należy zauważyć, że prędkość jest reprezentowana przez przebyty dystans podzielony przez ∆t, więc nie istnieje potrzeba wykorzystania fizycznego tachometru. Realizowane sprzętowo muszą być jedynie takie elementy układu jak enkoder, dwukierunkowy element logiczny, prosty licznik góra/dół oraz rejestr prędkościowego sprzężenia zwrotnego. Reszta operacji jest wykonywana programowo poprzez procesor.
Podczas ruchu zawartość licznika góra/dół przesyłana jest co okres ∆t do rejestru prędkościowego sprzężenia zwrotnego, po czym wartość licznika jest modyfikowana bez pominięcia jakichkolwiek impulsów. Oprócz generowania trajektorii pozycji procesor wykonuje także operacje mnożące i sumujące związane z pętlami regulacyjnymi wszystkich osi.
Zadania komputera i kart procesorowych
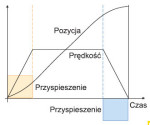
Rys. 6. Powstawanie trajektorii pozycji
Poszczególne pętle pozycji, prędkości i przyspieszeń realizowane mogą być w każdej osi przez pojedynczą kartę procesorową.
Zadaniem komputera jest wygenerowanie trajektorii ruchu poprzez stworzenie strumieni rozkazów, które przekazywane są do elementów wykonawczych każdej osi. Należy zauważyć, że dane rozkazów zawierają pozycje bezwzględne oraz, opcjonalnie, prędkości i przyśpieszenia, które mogą być wykorzystywane do bardziej precyzyjnego sterowania ruchem. Sygnały te nie są jednak od siebie niezależne, ponieważ np. pozycja odpowiada całce z prędkości.
Zadania komputera oraz kart procesorowych są schematycznie przedstawione na rys. 5. W komputerze można także zaprogramować ruch próbny, optymalizujący rozkazy impulsowe, co ma na celu minimalizację ewentualnego przeregulowania.
Przykład wykorzystania
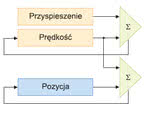
Rys. 7. Sposób generowania trajektorii oraz rejestry przyśpieszenia i prędkości
Jednym z najczęściej używanych rozkazów w sterowaniu ruchem jest przemieszczenie z pozycji aktualnej do docelowej. Użytkownik może określić położenie końcowe, maksymalną prędkość oraz przyśpieszenie i opóźnienie podczas startu i końca ruchu. Na rys. 6 przedstawiono zależność pozycji względem czasu, która została wyprowadzona z przyśpieszenia i maksymalnej prędkości. Na początku ruchu występuje stałe przyśpieszenie, które całkowane w czasie powoduje liniowy wzrost prędkości. Dzięki całkowaniu prędkości otrzymuje się trajektorię pozycji. Po osiągnięciu maksymalnej prędkości, przyśpieszenie ustaje a pozycja zaczyna rosnąć w sposób liniowy. W czasie opóźnienia, w odpowiednim rejestrze przyspieszenia umieszczana jest wartość ujemna, dzięki czemu prędkość zaczyna liniowo spadać.
Do realizacji sterowania wystarczające jest przekazywanie do kart procesorowych każdej osi (co okres ∆t) jedynie danych dotyczących nowych pozycji, ponieważ wartości prędkości i przyspieszeń można uzyskać bezpośrednio przez różniczkowanie. Jeśli jednak wymagane jest utrzymywanie bliskiego zeru błędu śledzenia, jako dodatek do danych pozycji mogą zostać użyte pomocnicze rozkazy dotyczące prędkości i przyspieszeń. Na rys. 7 przedstawiono sposób generowania trajektorii za pomocą komputera. W bardziej złożonych przypadkach pokazany na rysunku rejestr przyśpieszenia może również zmieniać się w czasie. Na przykład w ruchu po okręgu sparametryzowane pozycje x i y przyjmą odpowiednio wartości Rcos(t) i Rsin(t), a prędkości i przyśpieszenia będą także funkcjami sinus i cosinus.
Grzegorz Michałowski




















