Podstawy reakcyjnej i predykcyjnej regulacji PID - Część 2

PREDYKCYJNA REGULACJA PID

Regulacja reakcyjna bazuje całkowicie na wartości uchybu, w rzeczywistości jednak oczekiwane byłoby szybkie ustalenie wymaganego sygnału sterującego oraz wykorzystanie uchybu tylko do ewentualnej korekcji relatywnie mniejszej niedokładności predykcji.

Taki właśnie cel przyświeca regulacji predykcyjnej, która na podstawie obserwacji wartości zadanej próbuje przewidzieć sygnał sterujący wymagany do jej śledzenia. Ponadto, ponieważ regulator predykcyjny nie znajduje się w pętli sterującej, zapewnia zarówno większą szybkość, jak i lepszą stabilność niż regulacja reakcyjna.

ZALEŻNOŚĆ SYGNAŁU STERUJĄCEGO OD WARTOŚCI ZADANEJ

Można zauważyć dwie prawidłowości wiążące wartość zadaną z wymaganym sygnałem sterującym. Pierwsza jest taka, że dla każdej temperatury w stanie ustalonym wymaga się pewnej wartości sygnału sterującego (dostarczanej mocy), która przezwycięży utratę ciepła do otoczenia i utrzyma osiągniętą temperaturę. W przypadku aplikacji napędowych będzie to moc wymagana do przezwyciężenia oporów ruchu i utrzymania stałej prędkości.

W takiej sytuacji istotnych jest wiele czynników, takich jak np. temperatura otoczenia, jednak jeśli temperatury operacyjne wynoszą setki stopni, a temperatura otoczenia waha się np. w zakresie 20°, to można przyjąć, że stosunek wymaganego sygnału sterującego do wartości zadanej jest stały.

Druga prawidłowość dotyczy nachylenia wartości zadanej, czyli jej pochodnej. Dla serwonapędu położenia pochodna wartości zadanej określa zadaną prędkość, a druga pochodna – zadane przyspieszenie. Jeśli wartość zadana jest dodatnia, to należy dodać węgla do pieca lub przyspieszyć robota. Składowa różniczkująca jest zatem proporcjonalna do pochodnej wartości zadanej, a współczynnik proporcjonalności jest określany mianem wzmocnienia prędkościowego lub różniczkowego. Natomiast współczynnikiem proporcjonalności części podwójnie różniczkującej jest wzmocnienie przyspieszeniowe. Znajomość wartości tych wzmocnień pozwoliłaby serwonapędowi na dokładne śledzenie wartości zadanej z minimalnym możliwym opóźnieniem.

Wielką zaletą części różniczkującej wartość zadaną w stosunku do części różniczkującej uchyb jest to, że nie wzmacnia zaburzeń występujących w układzie.

ŁĄCZENIE REGULACJI REAKCYJNEJ I PREDYKCYJNEJ

Niestety regulacja predykcyjna nie umożliwia dokonywania korekt uwzględniających zmiany temperatury otoczenia lub obciążenia serwomechanizmu. Jest również mało prawdopodobne, że odpowiednio dobrane wartości współczynników będą właściwe dla każdego przypadku. Nie należy zatem oczekiwać wyjątkowej jakości w układzie regulacji predykcyjnej. Z tego powodu optymalne może być połączenie klasycznej regulacji PID z regulacją predykcyjną, jak np. w układzie przedstawionym na rysunku 4.

 

Rys. 4 Hybrydowy układ regulacji reakcyjno-predykcyjnej

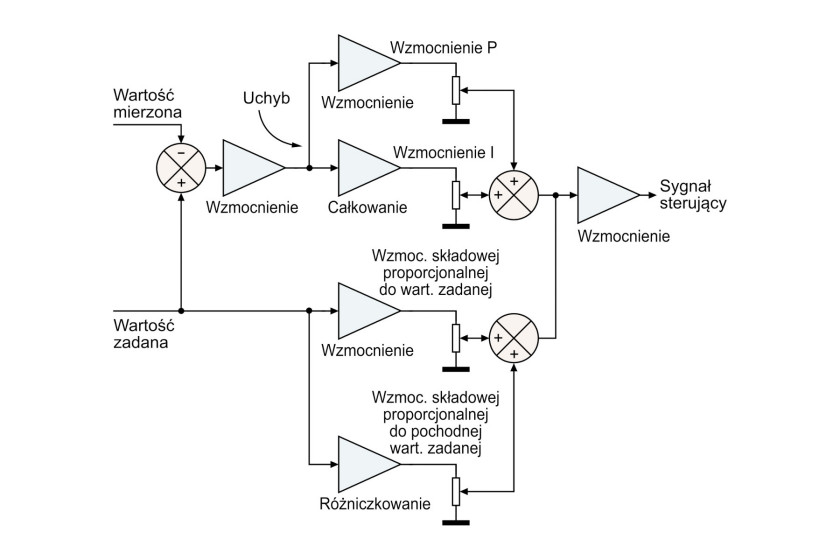
W tej konfiguracji chwilowa wartość zadana jest mnożona przez współczynnik wzmocnienia, czego wynikiem jest składowa proporcjonalna do wartości zadanej, która odpowiada za większość potrzebnego sygnału sterującego w stanie ustalonym.

Drugim nowym elementem regulatora jest różniczkowanie chwilowej wartości zadanej. Dodanie do siebie obu tych składowych pozwala na znacznie dokładniejsze ustalenie sygnału sterującego, czyli mocy wymaganej do przejścia z jednej wartości zadanej na drugą.

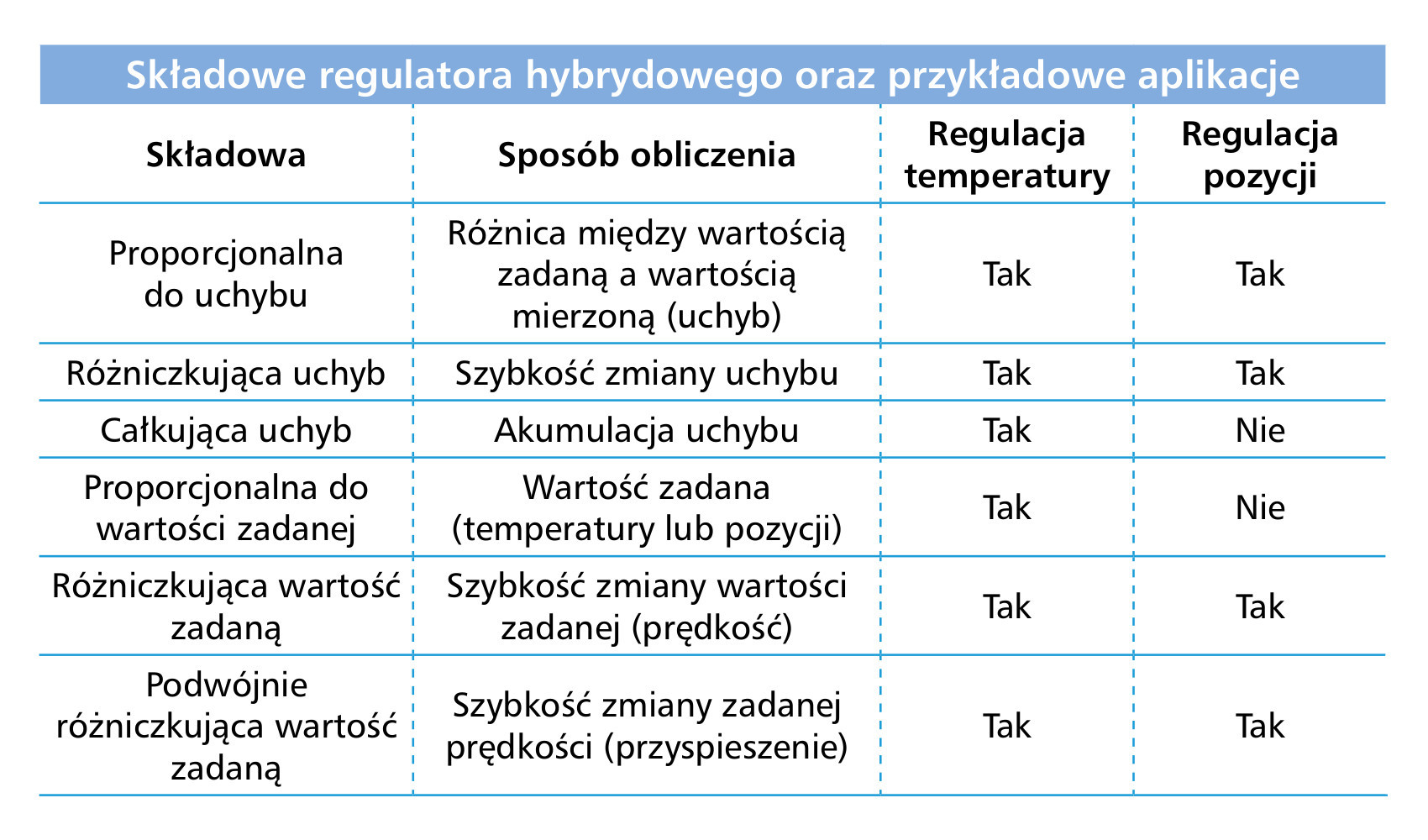
Ponadto zachowane zostały składowe sterowane przez uchyb – proporcjonalna i całkująca – celem zrównoważenia ewentualnych niedokładności predykcji. Wynikiem jest prosta architektura o wyjątkowych możliwościach dla szerokiego zakresu aplikacji. W tabeli przedstawiono składowe hybrydowego układu regulacji reakcyjno-predykcyjnej wraz z wyszczególnieniem aplikacji, w których mogą być przydatne.

POPRAWA JAKOŚCI REGULACJI PID

Ponieważ standardowy algorytm regulacji PID jest daleki od ideału, powstało wiele modyfikacji tego typu sterowania. W większości przypadków polegają one na zamianie omawianych współczynników wzmocnienia na wartości wyznaczone na podstawie tabel lub prostych funkcji. Jednym z najczęstszych problemów jest niesymetria odpowiedzi układu względem sygnału sterującego. Na przykład grzejnik może być w stanie szybko zwiększyć temperaturę, wykorzystując np. 30% mocy, jednak jeśli taka sama moc zostanie odjęta, temperatura może nie spaść w tak szybkim tempie, jak rosła. Powodem tej asymetrii jest fakt, że chłodzenie nie wynika z "odjęcia mocy", lecz jest spowodowane przez zjawisko wymiany ciepła.

Sygnał sterujący ciężkim mechanizmem jest również bardzo asymetryczny. Podczas gdy przyspieszenie serwomechanizmu z reguły wymaga dodania znacznej mocy, odjęcie jedynie jej niewielkiej ilości wystarczy do uzyskania opóźnienia o takiej samej wartości. Zastosowanie w takim przypadku symetrycznego regulatora PID nie pozwoli na osiągnięcie zadawalającego ruchu do przodu bez powodowania przewrócenia się robota w momencie zmiany znaku wektora przyspieszenia. Sytuacja byłaby jeszcze bardziej skomplikana, gdyby robot przekroczył szczyt wzgórza i zaczął zjeżdżać po drugiej stronie. Dlatego w przypadku niesymetrycznych obciążeń, z reguły użyteczne jest stosowanie dwóch współczynników wzmocnienia, jednego dla wejść dodatnich, a drugiego dla ujemnych.

Inną przydatną modyfikacją reakcyjnych składników regulatora PID jest ograniczenie uchybu tylko do zakresu, w którym ich reakcja będzie proporcjonalna. Jeśli uchyb znajdzie się wewnątrz tego zakresu, to będzie mnożony przez współczynnik wzmocnienia. W przeciwnym razie zastosowane zostanie odpowiednie ograniczenie uchybu. Jest to szczególnie przydatne do zapobieżenia zjawisku wind-up w składowej całkującej.

DOBÓR NASTAW W UKŁADZIE REGULACJI TEMPERATURY

Na rysunku 5 przedstawione są przykładowe przebiegi sygnałów w układzie regulacji temperatury. Należy zauważyć, że wartość zadana jest dobrze śledzona dzięki dokładnej prognozie wartości wymaganego sygnału sterującego. Gdy temperatura zadana rośnie liniowo, jej składowa różniczkująca jest stała, a w miarę dążenia do wartości oczekiwanej wpływ wartości zadanej na wartość sygnału sterującego maleje. Z kolei składowa proporcjonalna do wartości zadanej reprezentuje moc wymaganą do utrzymania obecnej temperatury.

 

Rys. 5 Sygnały w układzie regulacji reakcyjno-predykcyjnej

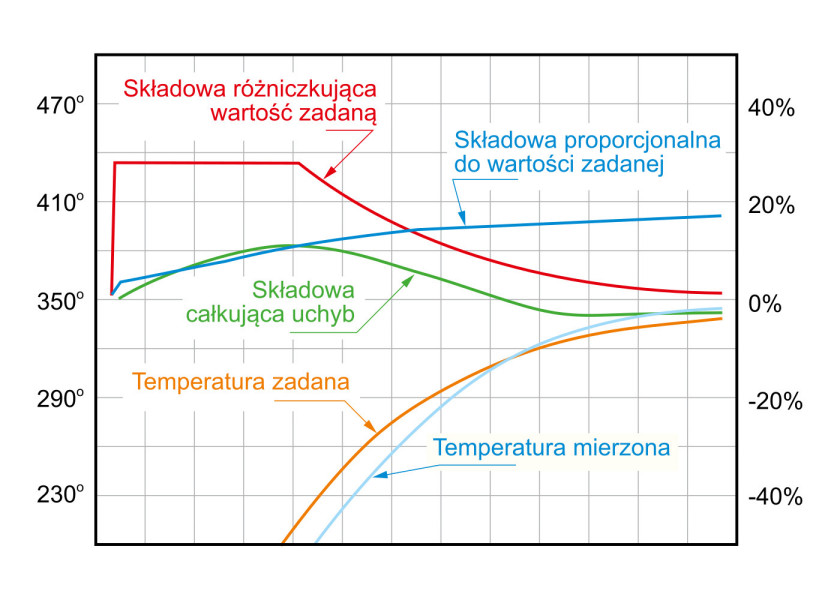
Składowa proporcjonalna do uchybu nie jest pokazana, jednak podobnie jak na rysunku 3 (patrz poprzedni artykuł) zmienia znak na przeciwny w chwili zrównania się temperatury mierzonej z jej wartością zadaną. Podwójny efekt składowej różniczkującej wartość zadaną oraz składowej proporcjonalnej do uchybu pomaga zapobiec przeregulowaniu.

Dobór nastaw regulatorów jest procesem iteracyjnym, który zwykle wymaga uruchomienia układu z jednym lub dwoma współczynnikami ustawionymi na zero. Po znalezieniu właściwych wartości wzmocnienia części proporcjonalnej i całkującej pozwala się, aby układ osiągnął stan ustalony w typowym punkcie pracy.

W stanie ustalonym składowa całkująca zastępuje składową proporcjonalną, a podzielenie jej przez wartość zadaną da szukany poziom współczynnika wzmocnienia wartości zadanej. Ponieważ składowa proporcjonalna do wartości zadanej równoważy moc dostarczaną wcześniej przez składową całkowania błędu, odpowiada to sytuacji, gdy rejestr całkujący jest opróżniony, a nowa składowa proporcjonalna generuje całość wymaganego sygnału sterującego.

Jeśli współczynnik wzmocnienia wartości zadanej był niezerowy, to w stanie ustalonym suma jej składowej proporcjonalnej i składowej całkowania błędu po podzieleniu przez wartość zadaną da poprawioną wartość szukanego współczynnika. Współczynnik wzmocnienia pochodnej wartości zadanej może być następnie wyznaczony poprzez wyzerowanie wszystkich innych współczynników oprócz współczynnika wzmocnienia wartości zadanej. Zmienia się wtedy wartość zadaną i ustawia taki współczynnik wzmocnienia pochodnej, aby nachylenie sygnału zadanego i mierzonego pokrywało się.

DOBÓR NASTAW W UKŁADZIE REGULACJI POZYCJI ROBOTA

W przypadku aplikacji serwonapędowych opisany proces określania współczynników może nie być odpowiedni. Regulatory silnika mogą być sterowane prędkością, jednak w robotach zadawana jest z reguły wartość pozycji, od ukształtowania której zależy zadana prędkość. W większości przypadków dokładność śledzenia prędkości nie jest tak istotna jak gładkość przebiegu prędkości zadanej.

Regulator do sterowania pozycją składa się głównie z następujących składowych proporcjonalnych: do zadanej prędkości, do zadanego przyspieszenia, do uchybu, oraz mniej ważnej składowej różniczkującej uchyb.

Ponieważ utrzymanie robota w miejscu na płaskiej powierzchni nie wymaga żadnej mocy, w takim przypadku nie ma potrzeby stosowania składowej proporcjonalnej do wartości zadanej. Na równi pochyłej składowa proporcjonalna do uchybu powinna zapobiec ruchowi po zatrzymaniu robota, a to wymaga stałego dostarczania mocy po osiągnięciu wartości zadanej.

DOKŁADNE ŚLEDZENIE WARTOŚCI ZADANEJ

Im gładszy przebieg wartości zadanej, tym jest bardziej prawdopodobne, że napęd będzie w stanie dokładnie ją śledzić. Z tego powodu nie zadaje się z reguły sygnałów w postaci funkcji, które nie są gładkie, gdyż wymagałoby to nieskończonego przyspieszenia w punktach nieróżniczkowalnych.

W bardziej skomplikowanych przypadkach nawigacyjnych znaczenie ma więcej kwestii niż tylko sterowanie w jednej osi. Konieczne jest wtedy m.in. rozwiązanie odwrotnego zadania kinematyki, które polega na przekształceniu zadanego przebiegu położenia robota w przestrzeni kartezjańskiej do przebiegów wartości zadanych każdego z jego silników.

PODSUMOWANIE

Regulacja PID wymaga znajomości fizyki i dynamiki sterowanych obiektów, a skuteczność ich realizacji zależy w połowie od wiedzy i instynktu. Jeśli zastosuje się podejście ściśle matematyczne, to określenie wartości wielu parametrów może być trudne, a otrzymany algorytm będzie bardzo wymagający obliczeniowo. Ponadto istotne jest użycie takiego oprogramowania, które umożliwi zmianę wartości praktycznie każdego składnika w trakcie pracy. Można wtedy obserwować odpowiedź układu na zmianę różnych parametrów. Należy również pamiętać, że nawet najbardziej skomplikowane układy składają się z wielu prostych bloków, więc jeśli te proste bloki zostaną dobrze poznane, to mogą posłużyć do tworzenia układów o bardzo złożonych zachowaniach.

Grzegorz Michałowski