Strojenie PID - metody doboru nastaw Część 1

Popularność regulatorów proporcjonalno-całkująco-różniczkujących - PID

Fot. 1. Przykładowy regulator PID i przykładowy blok w języku drabinkowym

Znaczna część urządzeń stosowanych w automatyce, takich jak sterowniki PLC czy przemienniki częstotliwości, jest wyposażona w funkcję regulacji sygnału wyjściowego za pomocą PID. Aby ułatwić konfigurację, wszystkie parametry takiego regulatora są zwykle zgrupowane wspólnie w menu urządzenia lub jego programie konfiguracyjnym. Na przykład sterowniki PLC programowane w języku drabinkowym mają specjalne bloki obsługujące regulator PID.

Na rynku dostępne są również samodzielne regulatory uniwersalne lub przeznaczone do regulacji temperatury. Są one przystosowane do montażu tablicowego albo na szynie DIN i mają wejścia analogowe do pomiaru zmiennej procesowej oraz wyjścia służące do regulacji urządzenia wykonawczego oraz sygnalizowania stanu regulatora. Konfiguracja jest możliwa za pomocą przycisków na obudowie lub, po podłączeniu komputera, za pomocą oprogramowania producenta. Jest ona prosta, polega na podaniu kilku parametrów. Niektóre regulatory wyposażone są w funkcję autotuningu.

Możliwości konfiguracji regulatorów implementowanych w urządzeniach automatyki są bardzo zróżnicowane. Począwszy od wprowadzenia podstawowych nastaw w najprostszych rozwiązaniach, aż po obszerne i skomplikowane zestawy parametrów dla rozbudowanych, wymagających aplikacji.

Jakość regulacji PID

Tabela 1.

Strojenie regulatora PID jest sztuką kompromisu. Osiągnięcie wszystkich celów stawianych układowi regulacji przez projektanta bywa niemożliwe. Przykładem może być szybkie osiągnięcie wartości zadanej przy jednoczesnym niewielkim przeregulowaniu. Aby osiągnąć wartość zadaną w krótkim czasie, należy przyłożyć do obiektu regulacji sygnał sterujący o dużej wartości.

Istnieje jednak zagrożenie, że wzrost wartości regulowanego sygnału nie wyhamuje po przekroczeniu wartości zadanej i osiągnie niepożądaną wartość, mającą niekorzystny wpływ na regulowany proces. Tego typu sprzeczności wynikają z parametrów fizycznych i technicznych elementów wykonawczych.

Dogłębna znajomość tych zagadnień ma kluczowe znaczenie dla doboru nastaw regulatora. Opracowano wiele kryteriów jakości regulacji, dzięki którym dopasowanie wymagań stawianych regulatorowi do możliwości regulowanego obiektu staje się łatwiejsze.

Pierwsza grupa kryteriów służy ocenie odpowiedzi układu na wymuszenie skokowe. Miarą dokładności osiągnięcia wartości zadanej jest uchyb ustalony (e_u), czyli wartość błędu po ustaniu procesów przejściowych. Czas regulacji jest opisywany dwoma ważnymi wskaźnikami, mianowicie czasem ustalania (t_r) i czasem narastania (t_n).

Pierwszy to czas pomiędzy przyłożeniem do układu wymuszenia a trwałym zmniejszeniem wartości uchybu poniżej wybranej niewielkiej wartości, która różnie definiowana wynosi zwykle kilka procent. Drugi to czas pomiędzy osiągnięciem 10% a 90% wartości zadanej. Niekorzystne dla procesu, duże przekroczenia wartości zadanej w początkowej fazie regulacji są opisywane przez przeregulowanie (M_p), czyli stosunek maksymalnej wartości odpowiedzi do wartości ustalonej.

Przy badaniu oscylacji układu pomocny jest również współczynnik zanikania (κ), to jest iloraz wartości bezwzględnych amplitud dwóch sąsiednich przeregulowań. Sposób wyznaczania powyższych parametrów został przedstawiony w dalszej części tekstu.

Kryteria całkowe zostały stworzone, aby wziąć pod uwagę cały przebieg sygnału błędu. Optymalizacja nastaw regulatora z ich wykorzystaniem polega na minimalizacji wartości jednego z następujących wskaźników jakości: ISE (Integral Squared Error), ITSE (Integral of Time multiplied by Squared Error), IAE (Integral of Absolute value of Error), ITAE (Integral of Time multiplied by Absolute value of Error).

Kryteria te służą raczej do symulacyjnego doboru nastaw, ze względu na praktyczne trudności związane z całkowaniem przebiegów uchybu rzeczywistych układów. Celem każdej regulacji jest osiągnięcie jak najmniejszej wartości błędu w możliwie najkrótszym czasie, dlatego zsumowanie całego uchybu jest dobrą miarą jej jakości - im mniejsza całka z uchybu, tym dokładniej jest odwzorowana wartość zadana.

Zwykła całka z uchybu nie jest jednak miarodajna, ponieważ w przypadku układu, w którym występują oscylacje, ujemne wartości błędu odejmowałyby się od dodatnich, w rezultacie dając mały wynik, pomimo dużych wahań zmiennej procesowej. Ze względu na to, w kryteriach całkowych stosowane są pewne przeliczenia powodujące uzyskanie jednego znaku wartości błędu i wprowadzające wagi dla dużych lub długotrwałych wartości.

Właściwości całkowych kryteriów jakości regulacji zostały zebrane w tabeli 1. Podane formuły zakładają całkowanie od zera do nieskończoności, jednak w praktyce wystarczające jest dobranie zakresu całkowania do momentu, w którym zanikną procesy przejściowe. W układach, w których uchyb ustalony jest równy zero, wskaźniki całkowe osiągają skończoną wartość.

Metody wyboru strojenia regulatorów PID

Opracowano szereg metod doboru nastaw, aby usprawnić żmudny i czasochłonny proces strojenia regulatorów PID. Przez wielu są uznawane za niepraktyczne i zbędne, jednak w sytuacjach, gdy istnieje możliwość ich wykorzystania, mogą być nieocenioną pomocą. Poniżej przedstawiono cztery z nich, wraz z przykładem zastosowania podczas komputerowej symulacji układu regulacji z członem inercyjnym pierwszego rzędu.

Dobór nastaw PID metodami Zieglera-Nicholsa

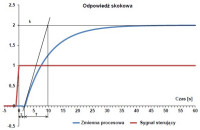
Rys. 1.

Metody Zieglera-Nicholsa zostały opracowane, aby pomóc w doborze nastaw regulatora PID korzystając z przebiegu odpowiedzi układu wyznaczonej doświadczalnie lub przez symulację. Nie jest wymagana dokładna znajomość modelu obiektu regulacji, co w znacznym stopniu upraszcza ich praktyczne wykorzystanie i zwiększa możliwości zastosowania.

Pierwsza metoda polega na aproksymacji parametrów odpowiedzi skokowej. Na rysunku 1 przedstawiona jest odpowiedź charakterystyczną dla wielu układów, które są opisywane członem inercyjnym. Jest ona typowa dla obiektów stosowanych w praktyce, co pozwala na uniwersalne stosowanie tej metody.

Odpowiedź tego typu układów można aproksymować charakterystyką skokową członu pierwszego rzędu z opóźnieniem transportowym, co umożliwia graficzne wyznaczenie parametrów, które są następnie wykorzystywane do obliczenia nastaw regulatora. Po wyznaczeniu charakterystyki skokowej należy wstawić linię styczną do przebiegu odpowiedzi w punkcie przegięcia.

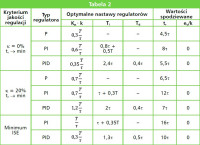
Tabela 2.

Następnie należy odczytać stałą czasową T i opóźnienie τ zgodnie z rysunkiem 1. Te dwie wielkości są podstawą do wyznaczania optymalnych nastaw regulatora. W tabeli 2 przedstawiono zestawy nastaw dla regulatorów P, PI oraz PID zoptymalizowane pod kątem spełnienia trzech różnych wymagań co do przebiegu odpowiedzi skokowej.

W pierwszym przypadku celem jest osiągnięcie odpowiedzi aperiodycznej (κ = 0%) przy minimalnym czasie ustalania (t_r › min). W drugim przypadku również wymaganiem jest minimalny czas ustalania (t_r › min), jednak dopuszczane są oscylacje (κ = 20%). W ostatnim przypadku założeniem jest minimalizacja kryterium całkowego ISE.

Analiza wartości spodziewanych przedstawionych w tabeli 2 pozwala na wyciągnięcie następujących wniosków. Najkrótszy czas ustalania powinien zostać zapewniony przez zestaw pierwszy (κ = 0%, t_r › min), zastosowanie tych nastaw jest związane jednak ze zgodą na największy uchyb ustalony w przypadku korzystania tylko z członu proporcjonalnego.

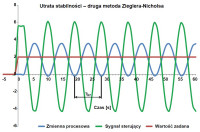
Rys. 2.

Korzyścią płynącą z implementacji tego rozwiązania jest całkowity brak oscylacji - wymaganie kluczowe dla wielu procesów. Jeśli w badanym układzie regulacji dopuszczalne są oscylacje, to osiągnięcie mniejszego uchybu ustalonego dla regulatora P jest możliwe dzięki wykorzystaniu drugiego zestawu nastaw (κ = 20%, t_r › min), należy jednak wziąć pod uwagę, że czas ustalania jest dłuższy niż w pierwszym przypadku.

W pewnych przypadkach najważniejszym wymogiem stawianym regulatorowi jest jak najwierniejsze odwzorowanie wartości zadanej. W takiej sytuacji najlepszym wyjściem może okazać się skorzystanie z zestawu parametrów minimalizującego ISE. Wadą tego rozwiązania jest najdłuższy czas ustalania spośród trzech omawianych wariantów.

Druga metoda jest łatwiejsza w stosowaniu sposobem doświadczalnym ze względu na brak konieczności wykreślania stycznej do przebiegu odpowiedzi w stanie nieustalonym. Aby wyznaczyć nastawy optymalne, należy doprowadzić układ do granicy stabilności, czyli momentu, w którym zaczynają się pojawiać niegasnące oscylacje. Jest to realizowane przez stopniowe zwiększanie współczynnika wzmocnienia K_p w układzie zamkniętym z regulatorem P.

Tabela 3.

Gdy układ zostanie doprowadzony do niegasnących oscylacji, przyjmuje się wzmocnienie krytyczne K_kr = K_p oraz mierzy się okres drgań krytycznych T_kr, jak zobrazowano na rysunku 2. Otrzymane współczynniki należy wstawić do wzorów z tabeli 3, aby otrzymać optymalne nastawy regulatora, którego przeregulowanie nie powinno przekraczać 30%.

Dobór nastaw PID metodą Cohena-Coona oraz Lambda

Pierwsza z metod jest bardzo podobna do tej Zieglera-Nicholsa, jednak daje dużo lepsze rezultaty w przypadku, gdy układ ma duże opóźnienie w stosunku do stałej czasowej. Wymagane jest wyznaczenie odpowiedzi skokowej układu otwartego (rys. 3), z której wylicza się parametry k_m, τ_m i d_m. Odpowiedź układu jest przybliżana odpowiedzią członu inercyjnego pierwszego rzędu z opóźnieniem transportowym. Optymalne nastawy są wyznaczane zgodnie z tabelą 4.

Rys. 3.

Tabela 4.

Metoda Lambda, w odróżnieniu od opisanych wcześniej, pozwala projektantowi na dobór nastaw w zależności od wymaganego przez niego czasu odpowiedzi (λ). Metoda została stworzona pod kątem zastosowania regulatora PI, a celem jest uzyskanie odpowiedzi aperiodycznej. Została ona opracowana dla kilku podstawowych członów automatyki, takich jak człon inercyjny i całkujący. Poniżej przedstawiono zastosowanie dla członu inercyjnego pierwszego rzędu.

W pierwszej kolejności wyznacza się charakterystykę skokową dla układu z otwartą pętlą sprzężenia zwrotnego i na jej podstawie oblicza się wartości służące do wyliczenia nastaw regulatora (rys. 4).

Rys. 4.

Tabela 5.

Następnie należy przyjąć stałą czasową λ, która będzie miarą szybkości reakcji układu na wymuszenie. Dla członu inercyjnego ustala się λ jako czas, po którym odpowiedź osiągnie 63% wartości zadanej. W tabeli 5 zawarte zostały wzory na nastawy regulatora wykorzystujące parametry odczytane z charakterystyki skokowej.

W drugiej części artykułu o regulatorach PID…

…przedstawione zostaną praktyczne aspekty wykorzystania omawianych metod, omówione będą także możliwe problemy oraz niekorzystne zjawiska, z którymi spotkać się można podczas strojenia regulatorów.

Piotr Ziółkowski