SIMATIC S7-1500T Technologia Motion Control od strony praktycznej. Część 9

MECHANIZM KRZYWKOWY

Znany już w XV wieku mechanizm krzywek jest układem mechanicznym pozwalającym na zamianę ruchu obrotowego (oś master) na nieliniowy ruch posuwisto-zwrotny (oś slave). Krzywka jest elementem mimośrodowym konstrukcji mechanicznej o specjalistycznym kształcie przenoszącym ruch wału na tzw. popychacz.

KRZYWKA MECHANICZNA

Rys. 1. Relacja krzywkowa

Przez wiele dekad mechanizm krzywkowy był stricte układem mechanicznym dającym szerokie możliwości przekazania pozycji jednego elementu na inny. Zmiana położenia może być jednorazowa lub okresowa. Przeznaczenie takich rozwiązań jest bardzo szerokie, sztandarowym przykładem zastosowania układu krzywkowego jest mechanizm rozrządu w silnikach spalinowych, stosowany do synchronicznego sterowania pracą zaworów.

Z punktu widzenia projektu układu krzywkowego zdefiniowanie wzajemnych przemieszczeń poszczególnych komponentów urządzenia to etap wstępny. Po wykonaniu konstrukcji mechanicznej należy wziąć pod uwagę obciążenie oraz eksploatację elementów wykonawczych, dopuszczalne przyspieszenia i potencjalne źródła błędów.

Inżynier musi więc obliczyć precyzyjnie ścieżkę ruchu dla każdego z podzespołów, aby zapewnić ciągłość pracy oraz zminimalizować zużycie mechanizmów. W wielu przypadkach poprawność wykonania projektu, doboru parametrów systemu czy optymalizacji układu napędowego może zostać stwierdzona dopiero po wykonaniu szeregu testów rozruchowych (np. o różnej częstotliwości), a także wytrzymałościowych na przestrzeni czasu.

Jeszcze do niedawna sprzężenia krzywkowe były intensywnie rozwijaną gałęzią inżynierii mechanicznej. W ostatnich latach tendencja ta uległa jednak diametralnej zmianie. Stało się tak przez bardzo dynamiczny rozwój technologii krzywek elektronicznych.

KRZYWKA ELEKTRONICZNA

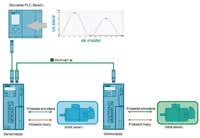
Rys. 2. Struktura systemu

Wykorzystanie nadrzędnego układu napędowego oraz mechaniczne przeniesienie ruchu jednostki głównej na krzywkowy aktuator wtórny pozwala na skoordynowany ruch synchroniczny o określonym profilu (funkcji). Rozwiązanie ściśle mechaniczne ma jednak sporo wad - dostrzegalnych zarówno na etapie konstrukcyjnym, jak i przy pracy oraz konserwacji maszyny. Jednorazowe zastosowanie projektu mechanicznego, zużycie elementów przeniesienia napędu czy kosztowne naprawy oraz rekonfiguracja - to tylko niektóre z utrudnień.

W związku z powyższymi niedogodnościami sprzężenie mechaniczne zostało zastąpione krzywką elektroniczną. Zamiast pojedynczego mechanizmu napędowego zastosowano dwa (lub więcej) niezależne napędy, które zostały zsynchronizowane odpowiednim profilem przez funkcję programową nadrzędnego systemu sterowania.

Inaczej mówiąc, użyty został nadrzędny sterownik oraz napędy serwo pracujące w układzie synchronicznym. Jest to dokładnie taki sam sposób sprzężenia elektronicznego osi, jaki poznaliśmy już w poprzednim rozdziale, z tym, że funkcja sprzęgająca nie jest relacją liniową, a dowolną funkcją zależności osi slave (nadążnej) względem osi master (wiodącej).

Zastąpienie sprzężeń mechanicznych krzywkami elektronicznymi znacznie poprawiło elastyczność rozwiązań, zwiększyło wydajność pracy maszyn oraz dało możliwość wprowadzania zmian do projektu na dowolnym jego etapie - bez konieczności przebudowy urządzenia.

Skomplikowane mechanizmy mogły zostać zastąpione jednym lub wieloma silnikami, które wykonywały odpowiedni ruch synchroniczny według zdefiniowanej funkcji. Kluczowa z punktu widzenia operatora okazała się możliwość zmiany produktu lub jego wariantu bez zatrzymania, a nawet spowolnienia produkcji dzięki możliwości swobodnej parametryzacji krzywek w trybie pracy systemu.

Cechy te dają nieograniczone możliwości projektowe, prowadzą również bezpośrednio do redukcji kosztów oraz znacząco ułatwiają programowanie i usprawniają serwisowanie maszyny.

KRZYWKI W SIMATIC S7-1500T

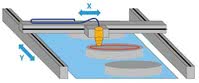
Rys. 3. Sprzężenie krzywkowe w układzie XY

Zgodnie z opisem z poprzednich publikacji - sterownik technologiczny SIMATIC S7-1500T pozwala na programową realizację trzech zasadniczych relacji synchronicznych: opisanych już wcześniej sprzężeń liniowych (relatywnego oraz absolutnego), a także krzywkowego. W zakresie rodziny sterowań S7-1500 - tylko jednostka technologiczna daje możliwość realizacji tego ostatniego zadania.

Poza koniecznością posiadania jednostki z oznaczeniem "T" nie ma tutaj żadnych innych wymagań. Wystarczy środowisko inżynierskie w wersji V14 lub nowszej. Nie są wymagane żadne dodatkowe pakiety programowe ani komponenty sprzętowe - komunikacja napęd-sterownik realizowana jest przez zintegrowany port PROFINET z obsługą komunikacji w trybie izochronicznym. Część logiczna również zaszyta jest w jednostce centralnej.

ZASTOSOWANIE KRZYWKI ELEKTRONICZNEJ

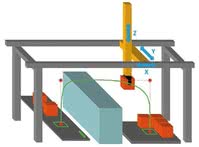
Rys. 4. Interpolacja ścieżki w układzie kartezjańskim XYZ

Mechanizm krzywkowy ma bardzo szerokie zastosowanie w różnego rodzaju aplikacjach. Wszędzie, gdzie wymagana jest nieliniowa relacja synchroniczna dwóch lub większej liczby osi, możemy zastosować sprzężenie krzywkowe. Przykładem może być wspomniana już w poprzednich dokumentach aplikacja piły latającej lub noża obrotowego, które zrealizować można zarówno przez prostą synchronizację osi, ale również przez stworzenie odpowiedniej funkcji dla sprzężenia krzywkowego.

Charakterystycznym przykładem mogą być również prasy lub urządzenia pakujące typu flowpack. Bardziej zaawansowane aplikacje, które również można zrealizować przez odpowiednią konfigurację relacji krzywkowych, to urządzenia do kreślenia lub wycinania kształtów (np. frezarka czy wycinarka laserowa lub wodna) w układzie kartezjańskim XY. Innym przykładem jest prosta interpolacja ścieżki w układzie kartezjańskim XYZ.

Wróćmy do przykładu z początku dokumentu, gdzie ruch obrotowy zostaje przemieniony w posuwisto-zwrotny. Klasyczne zastosowanie takiej konwersji można zaobserwować w prasach. Aplikacja prasy mimośrodowej (rysunek) to doskonała ilustracja takiego mechanizmu.

Ruch obrotowy mimośrodu przekłada się na przesunięcie stempla prasy, który dociskany jest do formy w momencie, gdy podajnik podsunie materiał w przestrzeń roboczą prasy. Mimośród stanowi tutaj klasyczne, mechaniczne przeniesienie ruchu obrotowego na liniowy, natomiast napęd mimośrodu oraz napęd podajnika to dwie niezależne jednostki, które synchronizowane są przez profil krzywkowy zdefiniowany w nadrzędnym sterowniku PLC.

W takim urządzeniu na jeden obrót napędu prasy (oś master) należy wygenerować przesunięcie podajnika od pozycji wyjściowej do pozycji końcowej (w przestrzeni roboczej prasy), a następnie jego powrót do pozycji bazowej. Cała maszyna pracuje zgodnie z cyklem pracy napędu master.

EDYTOR KRZYWEK

Edytor zależności pozycji osi nadążnej względem osi wiodącej pozwala na graficzną oraz tabelaryczną konfigurację punktów kluczowych, przez które ma przebiegać wykres funkcji, a także daje możliwość zaawansowanego określenia interpolacji, jaka pomiędzy tymi punktami (lub segmentami) ma zostać przez system zastosowana. Użytkownik ma również możliwość wskazania konkretnej funkcji łączącej dane punkty profilu.

Dzięki elastycznej obsłudze interfejsu użytkownika, swobodzie wprowadzania charakterystyki wejściowej, natychmiastowej analizie parametrów dynamicznych układu w środowisku inżynierskim - zyskujemy wyższą jakość ruchu, a także pełną elastyczność w konfiguracji naszego systemu.

PROFIL POZYCJI ORAZ JEGO POCHODNE

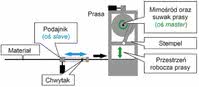
Rys. 5. Prasa mimośrodowa

W celu zdefiniowania przebiegu funkcji pozycji możemy korzystać z punktu, linii, sinusoidy, wielomianu oraz odwróconej sinusoidy .

Po wykreśleniu profilu krzywki możemy wybrać opcję wyświetlenia pochodnych funkcji pozycji - na jednym lub czterech osobnych trendach . Z matematyki wiemy, że pochodną funkcji jest zależność prędkości jej zmian względem jej argumentów. Argumentem naszej funkcji pozycji osi nadążnej jest pozycja osi wiodącej.

W związku z powyższym pierwszą pochodną profilu pozycji f(x) jest funkcja prędkości f’(x) (velocity), której argumentem będzie niezmiennie pozycja osi wiodącej. Druga pochodna pozycji f"(x) to relacja zmian prędkości względem pozycji, czyli przyspieszenie (acceleration). Natomiast trzecia f"’(x) to dynamika przyspieszenia, czyli tzw. zryw (jerk).

System oblicza i przedstawia powyższe przebiegi w formie graficznej w celu optymalizacji pracy układu. Funkcje te wykorzystywane są również celem interpolacji oraz mogą być wyznacznikiem ciągłości w celu wygładzenia profilu pozycji krzywki.

INTERPOLACJA SEGMENTÓW PRZEJŚCIOWYCH

Rys. 6. Edytor krzywek

Rysując przebieg profilu krzywki, korzystając z edytora graficznego - możemy wykonać go w sposób ciągły (bez luk wartości w pełnym zdefiniowanym zakresie) lub wstawiając jedynie segmenty (lub punkty), które są kluczowe dla naszej aplikacji. Odcinki nieokreślone mogą finalnie zostać zdefiniowane przez wybór funkcji matematycznej w tabeli edytora.

Dla każdego z nieokreślonych segmentów użytkownik może wybrać spośród dwóch metod interpolacji - VDI lub systemowej SIMATIC.

Zapraszamy do lektury styczniowego wydania magazynu, gdzie zamieszczony zostanie kolejny materiał z cyklu SIMATIC Motion Control. Będziemy w nim kontynuować opis zagadnień związanych z krzywkowym sprzężeniem osi. Zajmiemy się bardziej zaawansowanym podejściem do kwestii tworzenia funkcji sprzęgającej - opisem dostępnych metod optymalizacji, a także możliwością edycji profili podczas pracy aplikacji.

Siemens
www.automatyka.siemens.pl