SIMATIC S7-1500T - Technologia Motion Control od strony praktycznej. Część 10

INTERPOLACJA SEGMENTÓW PRZEJŚCIOWYCH

W poprzedniej publikacji omówiliśmy wstępnie możliwości edytora krzywek środowiska TIA Portal. Wspomnieliśmy wówczas o dwóch metodach optymalizacji - systemowej SIMATIC oraz tzw. VDI. Kontynuację tematu zacznijmy od wyjaśnienia tych pojęć.

INTERPOLACJA SYSTEMOWA

Rys. 1. Interpolacja liniowa

Rozważmy przykładowy profil krzywki, który został zdefiniowany przez 4 punkty w obszarze roboczym edytora graficznego. Wstawione punkty wyznaczają nam 3 segmenty, które wymagają interpolacji. Przykład ten może być bezpośrednim nawiązaniem do rozważanej aplikacji prasy (poprzednia publikacja), gdzie w pierwszej fazie cyklu podajnik z chwytakiem przesuwa materiał (np. blachę) w obszar roboczy prasy, tam - faza druga - prasa wykonuje swoje zadanie (np. wytłoczenie, zgrzewanie lub wycięcie), a w etapie ostatnim - powrót chwytaka do pozycji wyjściowej. Wszystkie etapy pracy osi nadążnej skoordynowane są w trakcie jednego obrotu wiodącej osi rotacyjnej prasy mimośrodowej.

Interpolacja liniowa (Linear interpolation)

Jest to szczególny przypadek aproksymacji za pomocą funkcji liniowej. W nawiązaniu do wcześniejszego opisu - w celach testowych wygenerujemy przebieg profilu pozycji wraz z jego pochodnymi (pozycja, prędkość, przyspieszenie, zryw).

Metoda jest bardzo prosta i nie generuje przekroczeń limitów, aczkolwiek w naszym przypadku powoduje nagłe zmiany dynamiki osi nadążnej, co będzie skutkować szarpnięciem układu (zwłaszcza przy większej prędkości).

Interpolacja funkcjami sklejanymi stopnia trzeciego (Interpolation with cubic splines)

Jest to metoda numeryczna polegająca na przybliżaniu nieznanej funkcji wielomianami niskiego stopnia. Algorytm ten jest często preferowany względem interpolacji wielomianowej ze względu na to, iż jego zastosowanie minimalizuje błędy aproksymacji.

W naszym przykładzie algorytm sprawdzi się o wiele lepiej niż aproksymacja liniowa - zmiana pozycji będzie znacznie bardziej wygładzona, aczkolwiek możemy zaobserwować, że w przypadku bezwarunkowej interpolacji (strona lewa) - podczas rekurencyjnego wywołania krzywki - nastąpi międzyfazowa nagła zmiana kierunku pracy osi (szarpnięcie). Z kolei w przypadku uwarunkowania ciągłością pierwszej pochodnej (strona prawa) przejście do kolejnego cyklu jest gładkie, zwróćmy jednak uwagę, że wyznaczona funkcja przekroczyła wyznaczony przez nas zakres wartości osi nadążnej.

Interpolacja krzywymi Béziera (Interpolation with Bézier splines)

Algorytm ten został opracowany w latach 60. przez francuskiego inżyniera firmy Renault. Krzywe Bézier-a są krzywymi parametrycznymi o charakterystyce wielomianowej. Znajdują szerokie zastosowanie w systemach optymalizacyjnych przetwarzania grafiki. Ze względu na cechy funkcji opisującej kształty, świetnie nadaje się także przy zagadnieniach optymalizacyjnych układów krzywkowych Motion Control.

Charakterystyczny dla optymalizacji krzywymi Bézier-a jest fakt, że wyznaczona funkcja nie przebiega przez wszystkie punkty wskazane do interpolacji. W przypadku 4 punktów określonych w naszym przykładzie - algorytm wyznacza krzywą (3. stopnia), która jest ograniczona przez jej styczne (w punkcie 1 oraz 4) wyznaczone przez pary punktów 1-2 oraz 3-4 (lewa strona - bez utrzymania ciągłości pierwszej pochodnej na skrajnych odcinkach profilu).

W naszym przykładzie ta metoda interpolacji wypada zdecydowanie najkorzystniej (zwłaszcza z uwzględnieniem utrzymania ciągłości prędkości na skrajnych odcinkach przebiegu - strona prawa) - nie powoduje przekroczeń zakresów wyznaczonych dla osi nadążnej, a także generuje optymalnie wygładzony kształt profilu.

W związku z charakterystyką algorytmu wadą jednak może okazać się fakt, że punkty 2 oraz 3 nie zostały ujęte w ścieżce osi nadążnej. Można to jednak zniwelować przez zmianę lokalizacji wyznaczonych wstępnie punktów lub przez połączenie różnych metod optymalizacji w konfiguracji przebiegu krzywki - o czym w dalszej części.

OPTYMALIZACJA VDI

Rys. 2. Interpolacja funkcjami sklejanymi stopnia trzeciego

Stowarzyszenie Inżynierów Niemieckich VDI (Verein Deutsche Ingenieure, www.vdi.eu) zdefiniowało wiele reguł w zakresie automatyzacji przemysłowej. Wśród nich znalazł się dokument (jeszcze z lat 80.) dotyczący standaryzacji zasad ruchu w układach ze sprzężeniem krzywkowym (VDI Guideline 2143 - Motion rules for cam mechanism). Wytyczne tej normy określają m.in. metodę optymalizacji profilu krzywki. Procedura znalazła miejsce jako alternatywa dla opcji systemowych proponowanych przez firmę Siemens.

Algorytm realizowany jest w oparciu o dwa wyróżniki:

• ciągłość wybranego parametru układu - pozycja, prędkość (bez wstrząsów), przyspieszenie (bez szarpnięć) lub zryw,
• cel optymalizacji (zgodnie z VDI) - brak określonego parametru, prędkość, przyspieszenie, zryw lub minimalna dynamika momentu.

Więcej informacji odszukać można w tematach pomocy systemowej TIA Portal lub w samej dokumentacji organizacji VDI.

Z praktycznego punktu widzenia - korzystając z algorytmów VDI - uzyskamy efekty bardzo podobne do omówionej w poprzedniej sekcji interpolacji systemowej. W związku z powyższym w niniejszej dokumentacji nie będziemy zajmować się szczegółową analizą efektów optymalizacji VDI. Warto mieć jednak na względzie, że pozwala ona (w przeciwieństwie do optymalizacji systemowej) na wybiórczą charakterystykę wskazanych segmentów, co można wykorzystać przy interpolacji mieszanej.

INTERPOLACJA MIESZANA

Rys. 3. Interpolacja krzywymi Béziera

Biorąc pod uwagę potrzeby naszej hipotetycznej aplikacji - możemy założyć, że wskazane będzie chwilowe zatrzymanie obrabianego materiału po jego podsunięciu w obszar roboczy prasy. Załóżmy więc, że po wykonaniu 160° obrotu osi wiodącej (prasa) nastąpi wykonanie zadania (np. zgrzewanie), co będzie wymagało zatrzymania osi nadążnej (podajnik) na 130° obrotu osi master. Po tym etapie następuje powrót podajnika do pozycji wyjściowej (zostaje na tę fazę 70° obrotu osi wiodącej).

Zastosowanie połączenia dwóch omówionych metod interpolacji pozwoli uzyskać pożądany efekt. Konkretnie - dla segmentu pierwszego (pomiędzy punktami 1-2) oraz dla segmentu trzeciego (wyznaczonego przez punkty 3-4) wybierzmy optymalizację systemową krzywymi Béziera (bez wymogu utrzymania ciągłości pierwszej pochodnej na odcinkach skrajnych). Z kolei dla segmentu środkowego (pomiędzy punktami 2-3) wybierzmy metodę VDI ze wskazaniem utrzymania ciągłości prędkości oraz bez określenia celu optymalizacji.

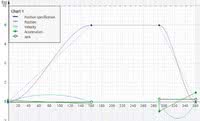
Rys. 4. Interpolacja mieszana

Powyższe ustawienia zaaplikowane dla naszego 4-punktowego przykładu spowodowały wygenerowanie następującego profilu krzywkowego.

Wynik interpolacji spełnia oczekiwania projektowe i wydaje się być optymalny z punktu widzenia dynamiki układu - nie ma przekroczeń zakresów, profil przechodzi przez wszystkie zdefiniowane punkty, a także prędkość ma charakterystykę ciągłą.

Czy rzeczywiście taki profil jest optymalny? Zależy to od wielu czynników. Dopiero wykonanie testów wytrzymałościowych (również długoterminowych) kompletnego systemu pozwoli określić zużycie elementów, zbadać drgania układu, jego reakcje na zmiany częstotliwości oraz dynamiki pracy czy oszacować jego żywotność.

EDYCJA KRZYWEK W PROGRAMIE PLC

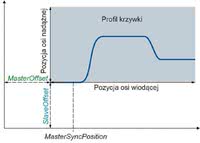
Rys. 5. Przesunięcie profilu krzywkowego

Na początku rozdziału wspomnieliśmy o możliwości edycji zdefiniowanych profili krzywkowych, również w trybie pracy systemu. Istotnie, w zależności od wymagań aplikacji możemy zastosować różne metody pozwalające na elastyczne dostosowanie parametrów sprzężenia do potrzeb produkcyjnych bądź uruchomieniowych.

Podczas budowania oraz testowania układu bardzo przydatna jest łatwość edycji parametrów krzywki - zarówno z poziomu środowiska inżynierskiego, jak i programu sterownika. Sterownik S7-1500T pozwoli nam na elastyczną modyfikację parametrów sprzężenia w celu usprawnienia fazy inżynierskiej.

Modyfikacja projektu to jednak nie wszystko - jeszcze więcej zalet dostrzeże w otwartości systemu użytkownik końcowy, który z łatwością będzie mógł samodzielnie dostosować tryb pracy urządzenia, nawet bez dostępu do środowiska narzędziowego oraz projektu.

Modyfikacja funkcji sprzęgającej w trybie pracy systemu sterowania daje możliwość przezbrojenia linii na inny produkt, modyfikacji parametrów wytwarzanego produktu, dostosowania do zmian podzespołów lub półproduktów, kalibracji układu, zmiany punktu odniesienia osi lub ich skalowania oraz wiele innych zależnych od aplikacji funkcji, które mogą zostać wdrożone nawet przy wykorzystaniu jedynie urządzenia HMI.

Skoncentrujmy się teraz na edycji profilu w trybie pracy systemu. Rozważmy kilka wariantów, które dostępne są w sterownikach serii S7-1500T.

STATYCZNA DEFINICJA OBIEKTÓW TECHNOLOGICZNYCH

Przyjmijmy, że konstruowana maszyna ma zostać przystosowana do wytwarzania wielu produktów lub jego wariantów, co wiązać się będzie bezpośrednio z koniecznością zmiany profilu sprzężenia osi skoordynowanych. Podstawową cechą systemu jest możliwość zdefiniowania wielu profili krzywkowych (tak jak wykonaliśmy to w poprzedniej sekcji), a następnie swobodna ich implementacja przez funkcje programu użytkownika. Taka metoda sprawdzi się w układach, gdzie będziemy w stanie określić zapotrzebowanie na konkretne funkcje krzywkowe, już na etapie inżynierskim.

Metoda ta, przy każdej zmianie profilu, wymagać będzie interpolacji oraz aktywacji krzywki, aczkolwiek definicja wielu obiektów technologicznych, co nie stanowi jednak żadnego problemu z technicznego punktu widzenia.

PRZESUNIĘCIE PROFILU

Rys. 6. Skalowanie profilu krzywkowego

Idąc krok dalej - załóżmy, że mamy zdefiniowane statycznie profile krzywek podobnie jak w powyższym przykładzie, z tym, że chcemy mieć również możliwość edycji tychże funkcji (przez program sterownika). Adaptacja profilu może odbywać się przez parametry funkcji sprzęgającej lub przez modyfikację technologicznego bloku danych. Zacznijmy od podstawowych, oraz łatwych w obsłudze, opcji dostępnych z poziomu funkcji interfejsu użytkownika.

Parametry funkcji programowej użytkownika (MasterOffset oraz SlaveOffset) pozwalają na zdefiniowanie wektora przesunięcia całego profilu na płaszczyźnie zależności osi wiodącej względem nadążnej. Mówiąc inaczej, możemy przesunąć punkt startowy profilu, a co za tym idzie - każdy kolejny, który został jednoznacznie wyznaczony podczas interpolacji. Sytuację ilustruje poniższa grafika.

Przesunięcie profilu nie wymaga ponownej interpolacji. Zmiana powyższych parametrów nie wprowadza zmian do krzywki zdefiniowanej w środowisku inżynierskim.

SKALOWANIE PROFILU

Poza możliwością przesunięcia całości zdefiniowanej funkcji, wraz z zakresem jej wartości oraz argumentów, funkcja systemowa umożliwia także zmianę „zagęszczenia” wartości względem osi układu współrzędnych. Innymi słowy, możemy rozciągnąć lub skurczyć zdefiniowany profil, czyli wykonać jego skalowanie.

Poniższe przebiegi czasowe ilustrują reakcję systemu na wybrane wartości parametrów skalujących zakres wartości osi wiodącej oraz nadążnej.

TWORZENIE KRZYWKI W TRYBIE RT

Rys. 7. Modyfikacja krzywki przez panel HMI

Powyższe metody z pewnością znajdą zastosowanie w systemach, gdzie liczba profili będzie ograniczona lub różne warianty produkcyjne będą wiązać się jedynie z wektorową lub proporcjonalną modyfikacją zdefiniowanych sprzężeń. Co w takim razie w przypadku, gdy zajdzie potrzeba stworzenia całkowicie nowego profilu krzywki?

Przejdźmy do najbardziej zaawansowanej oraz otwartej metody, jaką możemy tutaj wykorzystać, a mianowicie do swobodnej edycji profilu przez modyfikację obiektu technologicznego z poziomu programu sterownika.

Zacznijmy jednak od kilku zdań wstępu. Z poprzednich rozdziałów wiemy już, że każdy obiekt technologiczny, który wstawiamy do projektu, jest w rzeczywistości tzw. technologicznym blokiem danych, czyli blokiem danych, który ma zintegrowany interfejs usprawniający konfigurację, uruchomienie oraz diagnostykę osi. Pomijając jednak edytory graficzne, mamy do czynienia po prostu z blokiem danych. Łatwo zaobserwować to przez opis wstawionego do projektu obiektu technologicznego, który zawsze zawierają numer przydzielonego przez system DB.

Wartości zawarte w bloku danych mogą nam posłużyć do graficznej reprezentacji krzywki, np. na ekranie panelu operatorskiego. Kontynuując jednak drogę do edycji profilu - możemy tutaj również wykonać modyfikację parametrów sprzężenia. Zmiana wartości rekordów bloku danych, w środowisku inżynierskim nie przyniesie jednak oczekiwanego efektu, gdyż nadrzędnym źródłem danych jest edytor graficzny.

W związku z tym wszelkie zmiany zostaną przywrócone (do ustawień początkowych) podczas kompilacji projektu. Jesteśmy w stanie jednak trwale wpływać na zawartość technologicznego bloku danych w trybie pracy aplikacji. Możemy rozważyć tutaj wariant, gdzie profil mamy wstępnie zdefiniowany w środowisku inżynierskim lub utworzony został jedynie pusty obiekt technologiczny, który zostanie uzupełniony danymi podczas pracy systemu.

Modyfikacja krzywki od strony technologicznego bloku danych nie jest zadaniem prostym. Z pewnością wymaga szerokiej wiedzy - zarówno programistycznej, jak i znajomości technologii uruchamianego układu. Jest to oczywiście zadanie wykonalne, aczkolwiek wychodząc naprzeciw integratorom oraz użytkownikom końcowym firma Siemens przygotowała przykład aplikacji, który w łatwy sposób można wykorzystać do zrealizowania opisywanego zadania. Jest to gotowa biblioteka, która będzie doskonałą bazą do bezpośredniego wdrożenia w aplikacji ze sprzężeniem krzywkowym.

Szczegółowy opis zagadnienia, dokumentacja, a także przykładowy projekt można pobrać bez ograniczeń w następującej lokalizacji sieciowej: https://support.industry.siemens.com/cs/pl/en/view/105644659.

Opracowany przykład pozwala nie tylko swobodnie przekształcić profil krzywkowy w trybie pracy aplikacji, ale również daje możliwość wyświetlenia (np. na panelu operatorskim) aktualnie zaimplementowanego profilu.

Zapraszamy do lektury lutowego wydania magazynu APA, gdzie zamieszczony zostanie kolejny materiał z cyklu SIMATIC Motion Control. Zajmiemy się w nim opisem technologii szybkich wejść pomiarowych oraz precyzyjnych binarnych wyjść krzywkowych.

Siemens
www.automatyka.siemens.pl