Motion control, czyli jak tworzyć systemy serwonapędowe - część 1

CZĘŚĆ I - TROCHĘ TEORII

Rys. 1. Schemat blokowy serwonapędu

Główne komponenty serwonapędu przedstawiono na rysunku 1 - są to: sterownik ruchu, wzmacniacz (inaczej napęd), silnik z dołączonym obciążeniem oraz element pomiarowy w pętli sprzężenia zwrotnego (na przykład enkoder lub resolwer). Na rys. 2 zamieszczono uproszczony model serwonapędu opracowany z wykorzystaniem transformaty Laplace'a.

Serwosilnik został w nim przedstawiony z uwzględnieniem momentów bezwładności wirnika silnika oraz jego obciążenia J, tłumienia lepkościowego b, stałej momentu napędowego K_t oraz jego zaburzeń z zewnątrz T_d. Podstawowe bloki funkcjonalne sterownika ruchu to natomiast: generator trajektorii oraz regulator.

Generator trajektorii wyznacza profil ruchu, a na jego podstawie obliczane są wartości zadane parametrów ruchu podawane na wejście układu regulacji. Wzmacniacz przetwarza z kolei sygnał wyjściowy kontrolera ruchu na sygnał sterujący silnikiem. Moment napędowy silnika (T) jest proporcjonalny do jego prądu (I) i wynosi T ≈ K_t ⋅ I + T_d.

PID, PIV, SPRZĘŻENIE DO PRZODU

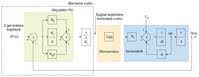
Rys. 2. Model serwonapędu

W kontrolerze wartość zadana położenia Θ*(s) obliczona w generatorze trajektorii jest porównywana z aktualną pozycją Θ(s) mierzoną przez enkoder lub inny czujnik sprzężony z wałem silnika.

Wynik tego zestawienia (błąd położenia) obliczany z zależności e(t) = Θ*(s) - Θ(s) jest sygnałem wejściowym bloku regulatora PID. Sygnał wyjściowy tego ostatniego jest obliczany jako suma trzech składników proporcjonalnych do sygnału błędu położenia, całki z sygnału tego błędu oraz jego pochodnej:

(t) = K_p ⋅ e(t) + K_i ⋅ ∫e(t)dt + K_d[de(t)/dt].

W razie potrzeby sygnał wyjściowy kontrolera ruchu jest odpowiednio przeskalowywany (blok 1/K^_r na rysunku 2).

Zadaniem projektanta serwosystemu jest dobór nastaw regulatora, czyli wyznaczenie współczynników bloków akcji proporcjonalnej K_p, całkującej K_i oraz różniczkującej K_d. Można to zrobić na kilka sposobów. Jednym z nich jest metoda prób i błędów, w której projektant bazuje głównie na własnym doświadczeniu. Można również skorzystać z jednej z metod analitycznych, na przykład Ziegera-Nicholsa.

Składa się ona z dwóch etapów. W pierwszym z nich współczynniki K_i oraz K_d należy wyzerować. Następnie układ pobudza się wymuszeniem skokowym, zwiększając przy tym wartość współczynnika K_p aż do momentu wystąpienia w układzie regulacji oscylacji. Wartości współczynnika K_o = K_p, przy którym to nastąpi oraz częstotliwości oscylacji f_o podstawia się następnie do wzorów: K_p = 0,6 · K_o, K_i = 2 · f_o · K_p oraz K_d = K_p/8 ⋅ f₀.

Na rysunku 3 przedstawia schemat serwonapędu z kontrolerem, którego częścią jest regulator PIV (Proportional position loop, Integral and proportional Velocity loop). Modyfikacja w stosunku do układu sterowania z rysunku 2 polega na dodaniu wewnątrz pętli regulacji położenia napędu pętli sterowania jego prędkością. Dobór nastaw regulatora PIV jest z reguły łatwiejszy niż w przypadku 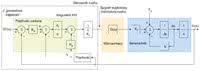regulatora PID.

Uzupełnieniem regulacji ze sprzężeniem zwrotnym jest sprzężenie do przodu. Przykład takiego połączenia zamieszczono na rysunku 4. Celem tego drugiego jest wyznaczenie momentu napędowego wymaganego do wykonania zadanego ruchu według zależności: T - Td = J · α* + b · ω*, gdzie α* to przyspieszenie, a ω* prędkość.

Wymaga to zamodelowania parametrów silnika oraz obciążenia (J^, b^). Ponadto ponieważ dokładna wartość T_d zaburzeń momentu napędowego nie jest znana, T można jedynie oszacować. Jeżeli T_d jest pomijalnie małe, oszacowanie to jest bardzo dokładne. Dzięki sprzężeniu do przodu skraca się czas reakcji układu regulacji, a prawdopodobieństwo przeregulowania jest mniejsze.

PROFILE RUCHU

Rys. 3. Regulator PIV

Na etapie doboru nastaw regulatora układ pobudza się wymuszeniem skokowym, podczas normalnej pracy serwonapędu korzysta się natomiast z profilu prędkości. Jednym z częściej wykorzystywanych jest profil trapezowy.

Jego popularność wynika stąd, że pozwala on dość łatwo wyznaczyć wszystkie niezbędne zmienne stanu, tzn. położenie, prędkość oraz przyspieszenie napędu. Równie popularny jest profil według krzywej S. Nazwy obydwu wynikają z podobieństwa kształtu ich wykresów prędkości w funkcji czasu do odpowiednich figur geometrycznych (rys. 5 a i b). Pierwszy profil składa się z trzech faz, natomiast drugi - aż z siedmiu.

Na rysunkach 5 c i d przedstawiono przebiegi przyspieszenia w funkcji czasu. Wynika z nich, że w wypadku profilu według krzywej S przyspieszenie najpierw liniowo wzrasta, aż do uzyskania maksymalnej wartości tej wielkości (faza 1). Utrzymuje się ono potem, aż do osiągnięcia odpowiedniej prędkości (faza 2). Wówczas przyspieszenie maleje (faza 3), aż do zera (faza 4). Gdy prędkość maleje, przyspieszenie jest ujemne i zmienia się liniowo (faza 5). Po uzyskaniu określonej wartości pozostaje stałe (faza 6), a później ponownie zmienia się liniowo, aż osiągnie zero (faza 7).

Profil trapezowy składa się natomiast tylko z faz: stałego przyspieszenia, stałej prędkości oraz stałego zwalniania, odpowiedników faz 2, 4 oraz 6 profilu według krzywej S. W tym wypadku nie ma zatem faz przejściowych zmiany przyspieszenia. Szybkość zmiany tej wielkości (jerk) jest w rezultacie w profilu trapezowym nieskończenie duża (teoretycznie), natomiast w profilu drugim ma wartość skończoną. Wpływa to na ich charakterystykę.

PROFIL TRAPEZOWY A KRZYWA S

Rys. 4. Układ sterowania z pętlami sprzężenia zwrotnego i do przodu

Im szybciej zmienia się przyspieszenie, tym większe drgania obciążenia mogą wystąpić. Ponieważ energia wibracji musi zostać zaabsorbowana, czas stabilizacji systemu wydłuża się, a dokładność sterowania jest mniejsza. Dlatego, mimo iż brak fazy przejściowej zmiany przyspieszenia powinien sprawić, że korzystając z profilu trapezowego szybciej można osiągnąć ustawienia docelowe, nie zawsze jest to prawdą.

W związku z tym w wielu zastosowaniach, w zależności od mechanicznych właściwości obciążenia i wymagań aplikacji, korzysta się z rozmaitych modyfikacji profilu według krzywej S. Na przykład dla maszyn pick & place, w których priorytetem jest duża szybkość, warto rozważyć zastosowanie profilu, gdzie fazy przejściowe 1, 3, 5 oraz 7 będą stanowiły 5-15% czasu trwania faz 2 i 6. Dzięki temu zmniejszą się oscylacje obciążenia. Z kolei, aby zwiększyć "gładkość" ruchu, można całkiem wyeliminować fazy 2 oraz 6.

Wybierając profil ruchu, uwzględnić trzeba również specyfikę silnika. Profile trapezowy i według krzywej S najlepiej sprawdzają się wtedy, gdy w szerokim zakresie zmienności prędkości moment napędowy zmienia się nieznacznie. W przeciwnym wypadku można skorzystać z profilu, w którym prędkość początkowa jest niezerowa (rys. 6 a) lub profilu parabolicznego (rys. 6 b).

CZĘŚĆ II - PRAKTYCZNE ASPEKTY DOBORU

WYBÓR TYPU SERWOSILNIKA

Rys. 5. Profile ruchu: trapezowy oraz według krzywej S

Ważnym etapem projektowania serwosystemu jest również wybór optymalnej kombinacji zespołu serwosilnik-serwowzmacniacz. Jest to proces wieloetapowy i niełatwy, a jednocześnie kluczowy dla sprawnego oraz efektywnego działania systemu sterowania ruchem.

Zanim rozpatrzone zostaną szczegółowe parametry różnych modeli, trzeba zdecydować, jaki rodzaj silnika najlepiej sprawdzi się w danym zastosowaniu. W serwosystemach korzysta się z silników skokowych, szczotkowych i bezszczotkowych prądu stałego (najczęściej) oraz asynchronicznych prądu przemiennego.

Te pierwsze mogą pracować z pełnym momentem w stanie spoczynku, a jednocześnie charakteryzuje je przystępny rozmiar oraz waga. Niestety im większa prędkość, tym ich moment napędowy jest mniejszy. Maksymalna prędkość sięga 5000 obr./min przy bardzo małym momencie obrotowym, moc tego typu silników wynosi natomiast do kilkuset watów.

Do ich wad zalicza się również wytwarzanie hałasu oraz wibracje. Niepożądane są zwłaszcza te ostatnie, które mogą wpływać na żywotność mechanicznych komponentów systemu. Aby ograniczyć drgania, stosuje się specjalne techniki sterowania (microstepping), można również skorzystać z amortyzatorów. Środki te jednak nie rozwiązują problemu drgań całkowicie.

Szczotkowe silniki prądu stałego sprawdzają się w szerokim zakresie aplikacji, zarówno w pozycjonowaniu, jak i w regulacji prędkości oraz momentu obrotowego. Dostępne są w wersjach o mocach sięgających kilku kW i prędkościach przekraczających 10 tys. obr./min. Pracują równo i cicho. Słabym punktem tego rodzaju silników są natomiast szczotki, które z czasem zużywają się i muszą być okresowo wymieniane. Ich pracy towarzyszy również zjawisko powstawania łuku elektrycznego. Wadą szczotkowych silników DC jest także mały moment obrotowy w stosunku do ich wymiarów oraz wagi.

SILNIKI BEZSZCZOTKOWE I INDUKCYJNE

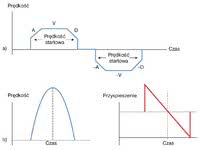
Rys. 6. Alternatywne profile ruchu: a) z niezerową prędkością początkową b) paraboliczny

Silniki bezszczotkowe DC są jednym z najczęściej używanych typów silników w systemach serwo. Do ich najważniejszych zalet zalicza się: równą i cichą pracę oraz to, że nie wymagają mechanicznej komutacji. Ich maksymalna prędkość przekracza 30 tys. obr./min. Wytwarzają też duży moment obrotowy, a przy tym ich wymiary i waga są do zaakceptowania w większości zastosowań.

Niestety urządzenia te mają również kilka istotnych wad. Przede wszystkim są droższe, co wynika stąd, że w celu uzyskania większego momentu obrotowego elementy ich konstrukcji są wykonane z magnesów ziem rzadkich (na przykład neodymowych lub samaro-kobaltowych). Ponadto ponieważ komutacja silników tego typu jest realizowana elektronicznie, wymagają one bardziej skomplikowanych, a przez to droższych wzmacniaczy.

Z kolei dzięki prostej konstrukcji zaletą silników asynchronicznych jest z kolei długa żywotność oraz stosunkowo niski koszt. Rzadko są one stosowane w pozycjonowaniu, natomiast coraz częściej w aplikacjach z regulowaną prędkością i momentem obrotowym.